- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике к уроку Показательная функция
Содержание
- 2. Показательная функция, уравнения, неравенства. Вабищевич С.Н. преподаватель
- 3. ЦЕЛЬ УРОКА :Обобщить и закрепить теоретические знания
- 4. Блиц – опрос1. Какая функция называется показательной?2.Свойства
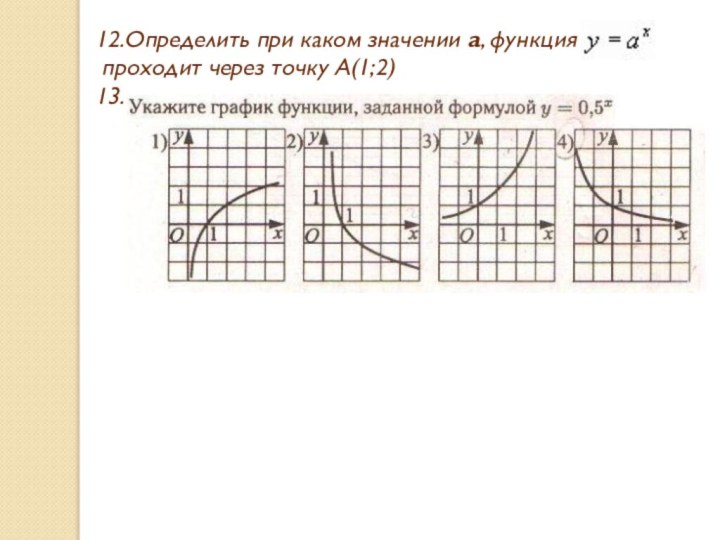
- 5. 12.Определить при каком значении а, функция проходит через точку А(1;2)13.
- 6. Показательная функция Определение.Функция, заданная формулой у =
- 7. Свойства показательной функциипри а>1: Область определения –
- 8. График показательной функции.При 0 1:
- 9. Свойства степениПри а >1, 0 < а
- 10. Показательные уравнения Показательными уравнениями называются уравнения вида
- 11. Способы решения показательных уравнений
- 12. Первый способПриведениеобеих частей уравнения к одному и
- 13. Второй способПутем введения новой переменной приводят уравнение
- 14. Третий способВынесение общего множителя за скобки.Пример:3х ––
- 15. Четвертый способ Пример: 4х = х +
- 16. Показательные неравенстваЕсли а > 1, то показательное
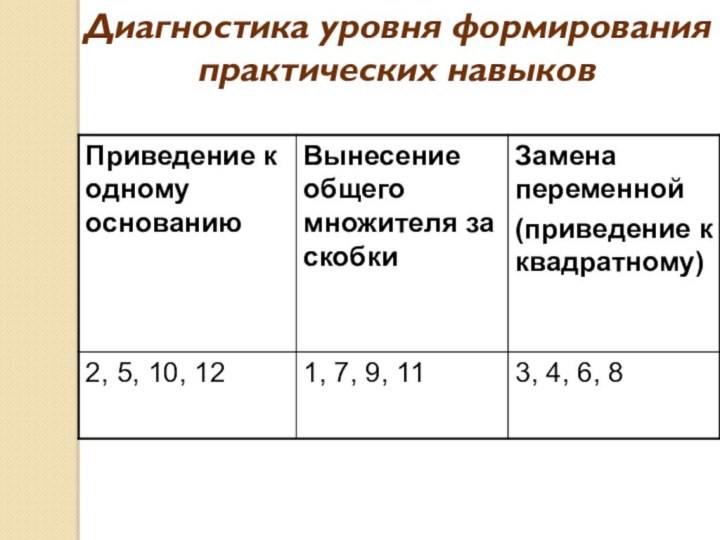
- 17. Указать способы решения показательных уравнений
- 18. Диагностика уровня формирования практических навыков
- 19. Решить показательные неравенства22х-4 > 64(0,2)х ≥ 0,04
- 20. Решение показательных неравенств22х-4 > 6422х-4 > 26 2х
- 21. Математический диктантФункция
- 22. Ответ- + - - +
- 23. В данном задании зашифровано имя математика, который впервые ввёл понятие показательная функция Разгадай ребус
- 24. Лейбниц Готфрид ВильгельмЛейбниц Готфрид Вильгельм – великий математик, который впервые ввёл понятие показательная функция
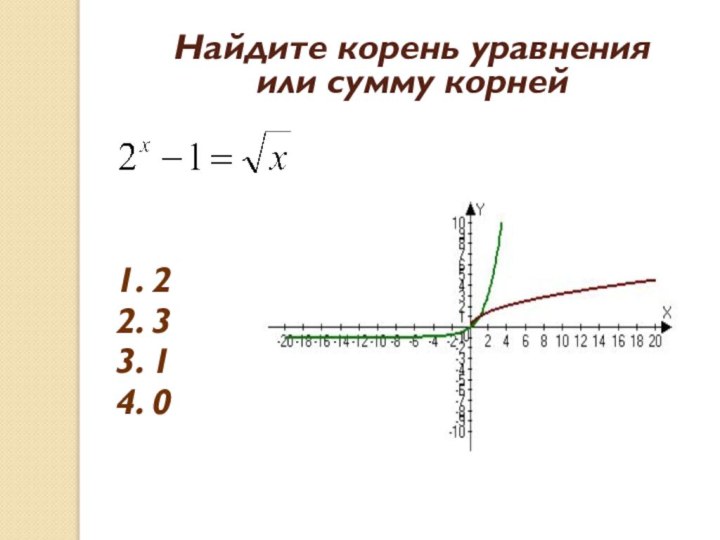
- 25. Найдите корень уравнения или сумму корней 1.22.33.14.0
- 26. Найдите корень уравнения или сумму корней 1. 22. 33. 14. 0
- 27. Решите неравенство
- 28. Решите неравенство
- 29. Решите неравенство
- 30. Решите неравенство
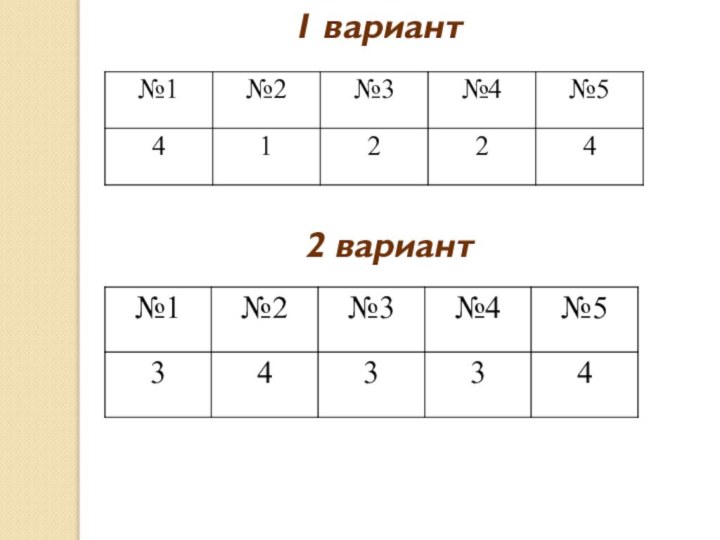
- 31. 1 вариант2 вариант
- 32. Скачать презентацию
- 33. Похожие презентации
Показательная функция, уравнения, неравенства. Вабищевич С.Н. преподаватель ФГКОУ НСВУ МВД России Новочеркасск 2018 г


























Слайд 3
ЦЕЛЬ УРОКА :
Обобщить и закрепить теоретические знания методов,
умения и навыки решения показательных уравнений и неравенств на
основе свойств показательной функции.Развивать монологическую речь, правильное оформление решений КИМов ЕГЭ, вычислительные навыки.
Воспитывать трудолюбие, терпение, усидчивость, умение слушать товарищей, работать в группе.
Слайд 4
Блиц – опрос
1. Какая функция называется показательной?
2.Свойства показательной
функции?
3.График показательной функции?
4.Свойства степени?
5. Какое уравнение называют показательным?
6.Способы
решения показательных уравнений?7.Показательные неравенства?
8.Как решать показательные неравенства?
9.Какова область определения функции у=0,3х?
10.Каково множество значений функции у=3х?
11.Возрастает или убывает показательная функция
Слайд 6
Показательная функция
Определение.
Функция, заданная формулой
у =
ах
(где а >0, а ≠ 1, х – показатель
степени),называется показательной
функцией с основанием а.
Слайд 7
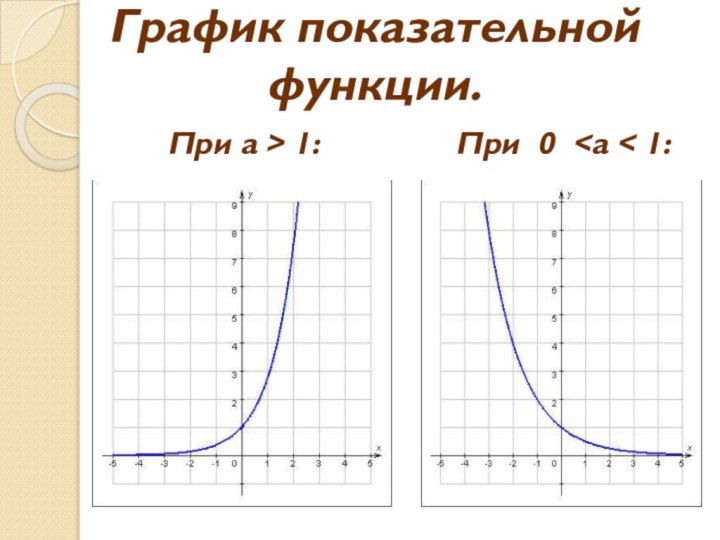
Свойства показательной функции
при а>1:
Область определения – множество
действительных чисел.
Область значений – множество положительных действительных чисел.
Функция возрастает на всей числовой прямой. При х = 0, у = 1, график проходит через точку (0; 1)
при 0 < а < 1:
Область определения – множество действительных чисел.
Область значений – множество положительных действительных чисел.
Функция убывает на всей числовой прямой.
При х = 0, у = 1, график проходит через точку ( 0 ; 1)
Слайд 10
Показательные уравнения
Показательными уравнениями называются уравнения вида
аf(x) = аq(x), где а – положительное число, отличное
от 1, и уравнения, сводящиеся к этому уравнению.
Слайд 12
Первый способ
Приведение
обеих частей уравнения к одному и тому
же основанию.
Пример:
2х = 32,
так как 32= 25, то имеем:
2х = 25
х = 5.
Слайд 13
Второй способ
Путем введения новой переменной приводят уравнение к
квадратному.
Пример: 4х + 2х+1 – 24 = 0
Решение:
Заметив , что 4х=(22 )х=( 2х)2 и 2х+1 = 2х × 21 , запишем уравнение в виде:
(2х )2 + 2×2х – 24 = 0,
Введем новую переменную 2х = у;
Тогда уравнение примет вид:
У2 + 2у – 24 = 0
Д = в2 – 4 а с = 22 – 4×1×(–24)
= 100> 0, находим у1 = 4, у2 = – 6.
Получаем два уравнения:
2х= 4 и 2х = – 6
22 = 22 корней нет.
х = 2.
Слайд 14
Третий способ
Вынесение общего множителя за скобки.
Пример:
3х –– 3х+3
= –78
3х –3х ×33 = –78
3х ( 1 –33
) = –783х ( – 26) = – 78
3x = – 78 : ( –26)
3х = 3
Х = 1.
Слайд 15
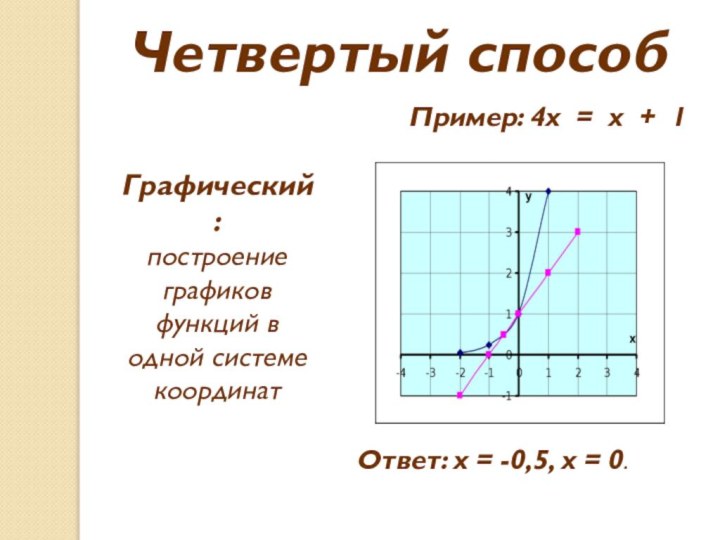
Четвертый способ
Пример: 4х = х + 1
Графический:
построение графиков функций в одной системе координат
Ответ: х =
-0,5, х = 0.
Слайд 16
Показательные неравенства
Если а > 1, то показательное неравенство
аf (x) > аg (x) равносильно
неравенству того же смысла f(x) > g(x).
Если 0 < а < 1 , то показательное неравенство
аf (x) > аg (x) равносильно неравенству противоположного смысла
f(x) < g(x).
Слайд 20
Решение показательных неравенств
22х-4 > 64
22х-4 > 26
2х –
4 > 6
2х > 10
х >
5Ответ: х > 5
(0,2)х ≥ 0,04
(0,2)х ≥ (0,2)2
х ≤ 2
Ответ: х ≤ 2
Слайд 21
Математический диктант
Функция
- возрастающая
Функция
- возрастающаяРешением неравенства -
является X<5
Решением неравенства -
является X<3
Решением неравенства -
является





























