- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методы решения планиметрических задач
Содержание
- 2. Метод площадей в решении задач Квасова О.Д.,учитель математики ВКК
- 3. Основные свойства площадей Свойство №1Если вершину треугольника
- 4. Свойство №2 Если два треугольника имеют одинаковые
- 5. Свойство №3 Если два треугольника имеют общий
- 6. Свойство №4 Площади треугольников, имеющих равные стороны, относятся как соответствующие этим сторонам высоты.
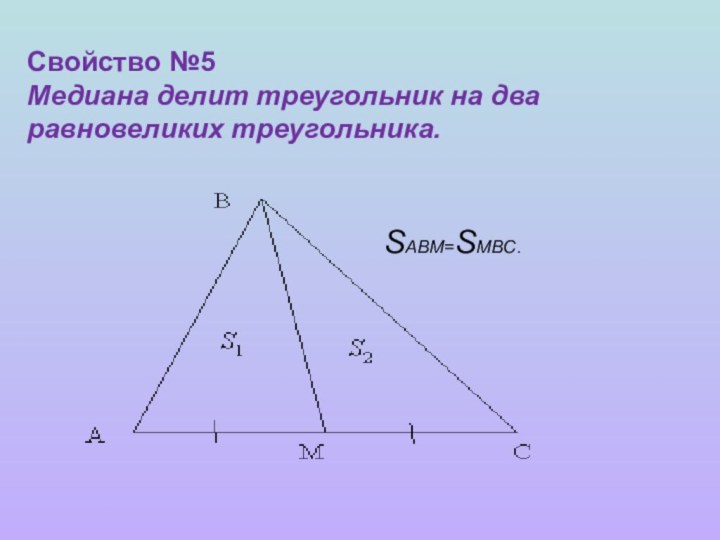
- 7. Свойство №5 Медиана делит треугольник на два равновеликих треугольника.SABM=SMBC.
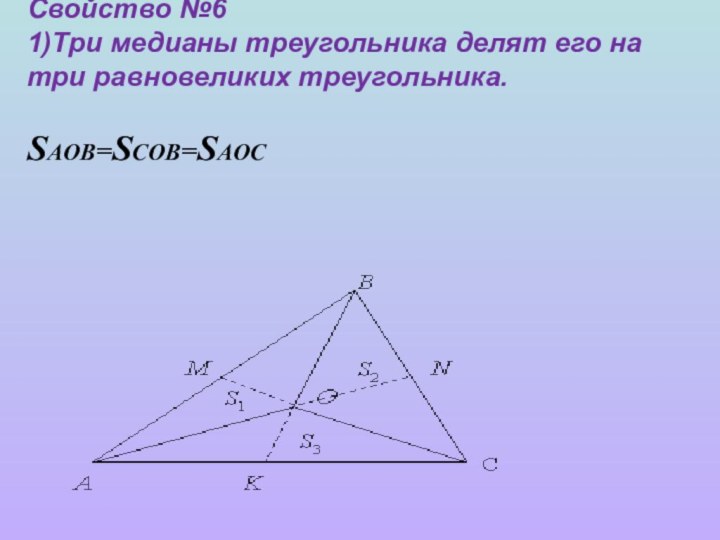
- 8. Свойство №6 1)Три медианы треугольника делят его на три равновеликих треугольника. SAОВ=SСОВ=SAОС
- 9. 2)Три медианы треугольника делят его на шесть равновеликих треугольников.
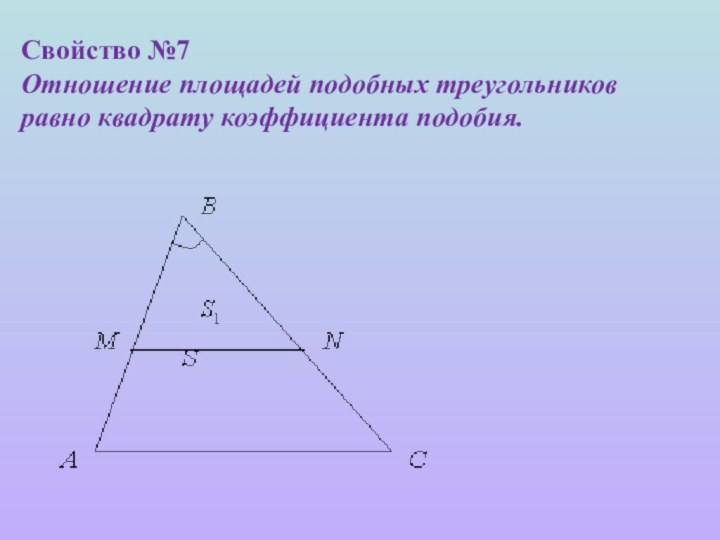
- 10. Свойство №7 Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
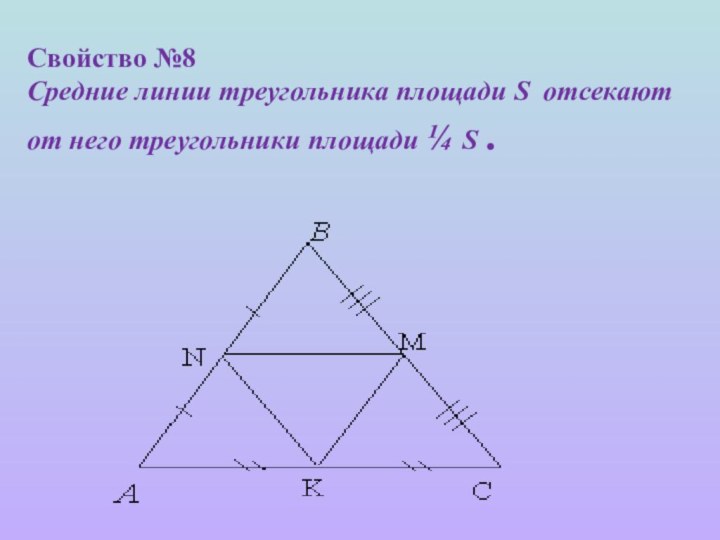
- 11. Свойство №8 Средние линии треугольника площади S отсекают от него треугольники площади ¼ S .
- 12. Задача1 Дано: ABCD - параллелограмм, ВМ=МС, SAВM=4
- 13. Задача 2 Дано: ABCD– параллелограмм, АК=КD
- 14. Задача 3 Найти расстояние от точки пересечения
- 15. Задача 4 Через середину K медианы BM треугольника ABC и вершину A проведена
- 16. Утверждение 1 В четырехугольнике ABCD стороны AD
- 17. Обратное утверждениеДано: AD║BC.Доказать: SΔAOB=SΔCOD.Доказательство.1. SΔAOB=SΔABC – SΔBOC,
- 18. Утверждение 2 В выпуклом четырехугольнике ABCD выполняется равенство
- 19. Задача 5 В треугольнике АВС проведена
- 20. Задача 6 Диагонали выпуклого четырехугольника ABCD
- 21. Скачать презентацию
- 22. Похожие презентации












Слайд 3
Основные свойства площадей
Свойство №1
Если вершину треугольника передвигать по
прямой, параллельной основанию, то площадь при этом не измениться.
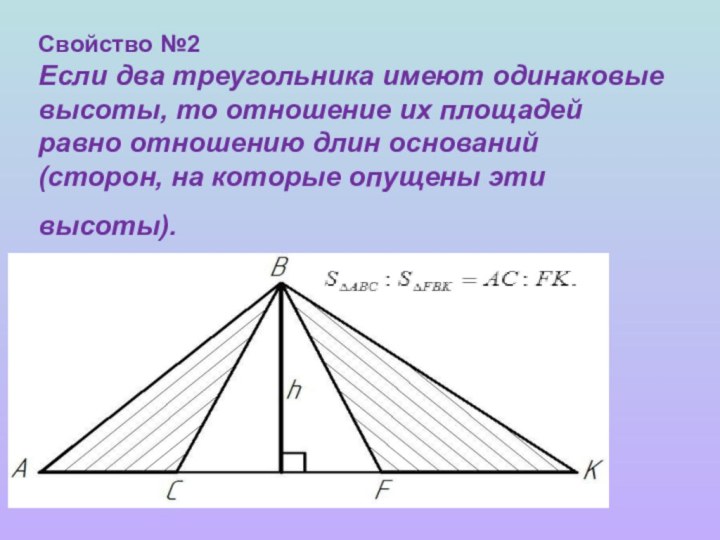
Слайд 4 Свойство №2 Если два треугольника имеют одинаковые высоты, то
отношение их площадей равно отношению длин оснований (сторон, на
которые опущены эти высоты).Слайд 5 Свойство №3 Если два треугольника имеют общий угол (или равный
угол), то их площади относятся как произведение сторон, заключающих
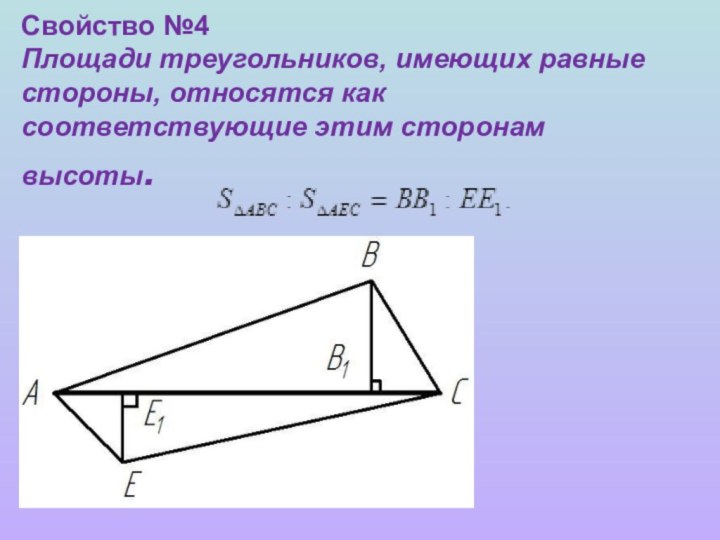
этот угол.Слайд 6 Свойство №4 Площади треугольников, имеющих равные стороны, относятся как
соответствующие этим сторонам высоты.
Слайд 8 Свойство №6 1)Три медианы треугольника делят его на три
равновеликих треугольника.
SAОВ=SСОВ=SAОС
Слайд 11 Свойство №8 Средние линии треугольника площади S отсекают от него
треугольники площади ¼ S .
Слайд 12
Задача1
Дано: ABCD - параллелограмм, ВМ=МС, SAВM=4
Найти: SAMD
SAMD= ½
SABCD
SABM + SCMD= ½ SABCD =8
SABM = SCMD
SAMD=8
Слайд 13 Задача 2 Дано: ABCD– параллелограмм, АК=КD BK ∩ AC
= N,
Найти: SABN
(свойство №6
(1))SABN=10
Слайд 14 Задача 3 Найти расстояние от точки пересечения медиан прямоугольного
треугольника до его гипотенузы, равной 25 см, если один
из катетов равен 20 см.Дано: ΔАВС (∠ А=90), ВС=25см, АВ=20см.
О - точка пересечения медиан,
ОК ВС
Найти: ОК.
Решение:
ΔАВС (∠ А=90). По теореме Пифагора АС=15.
2. О - точка пересечения медиан,
SOLC = SABC / 6; (свойство №6 (2))
SOLC = 150/ 6; SOLC = 25
3. С другой стороны SOLC = 1/2LC · OK;
OK = 2 SOLC / LC; OK = 4 см.
Ответ: 4см.
Слайд 15 Задача 4 Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC
в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Решение.
Проведём
отрезок MT, параллельный AP. Тогда MT — средняя линия треугольника APC и CT = TP, а KP — средняя линия треугольника BMT и TP = BP.Обозначим площадь треугольника ВKP через S . Тогда SΔКРС =2S, т.к. треугольник KPС, имеет ту же высоту и вдвое больше основание.
Значит, SΔСКВ = SΔСКМ = 3S (CK – медиана треугольника СМВ).
SΔСКМ = SΔАКМ = 3S (KМ– медиана треугольника АКС). SΔABК = SΔАКМ = 3S (AK – медиана треугольника AМВ).
Итак, SKPСM = SΔСКМ +SΔКРС=5S. SΔABК =3S
Значит, SΔABК: SKPСM =3:5=0,6
Ответ: 0,6.
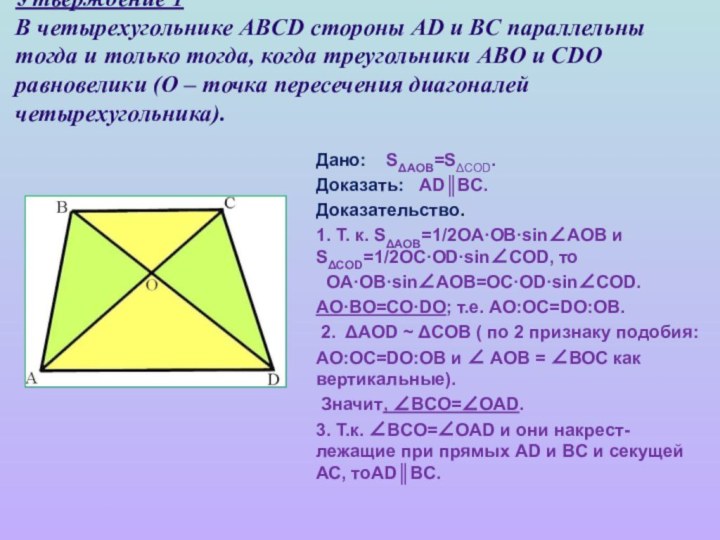
Слайд 16 Утверждение 1 В четырехугольнике ABCD стороны AD и BC
параллельны тогда и только тогда, когда треугольники ABO и
CDO равновелики (О – точка пересечения диагоналей четырехугольника).Дано: SΔAOB=SΔCOD.
Доказать: AD║BC.
Доказательство.
1. Т. к. SΔAOB=1/2OA·OB·sin∠AOB и SΔCOD=1/2OC·OD·sin∠COD, то
OA·OB·sin∠AOB=OC·OD·sin∠COD.
AO·BO=CO·DO; т.е. AO:OC=DO:OB.
2. ΔAOD ~ ΔCOB ( по 2 признаку подобия:
AO:OC=DO:OB и ∠ АОВ = ∠ВОС как вертикальные).
Значит, ∠BCO=∠OAD.
3. Т.к. ∠BCO=∠OAD и они накрест-лежащие при прямых AD и BC и секущей АС, тоAD║BC.
Слайд 17
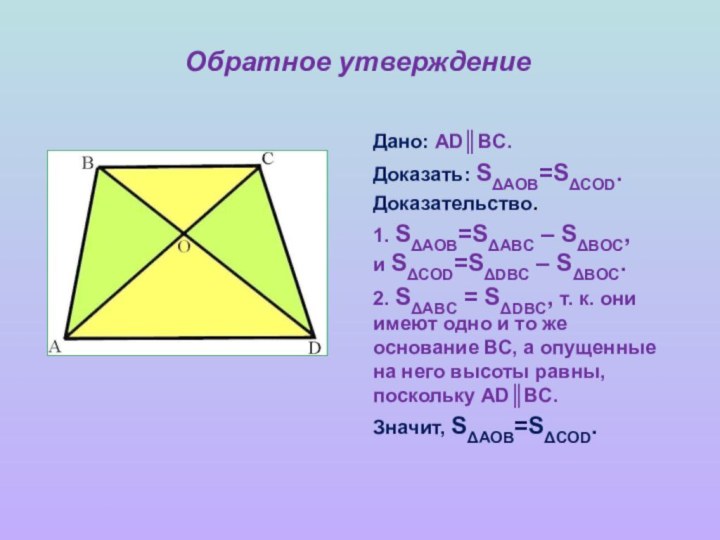
Обратное утверждение
Дано: AD║BC.
Доказать: SΔAOB=SΔCOD.
Доказательство.
1. SΔAOB=SΔABC – SΔBOC,
и SΔCOD=SΔDBC
– SΔBOC.
2. SΔABC = SΔDBC, т. к. они имеют
одно и то же основание ВС, а опущенные на него высоты равны, поскольку AD║BC. Значит, SΔAOB=SΔCOD.
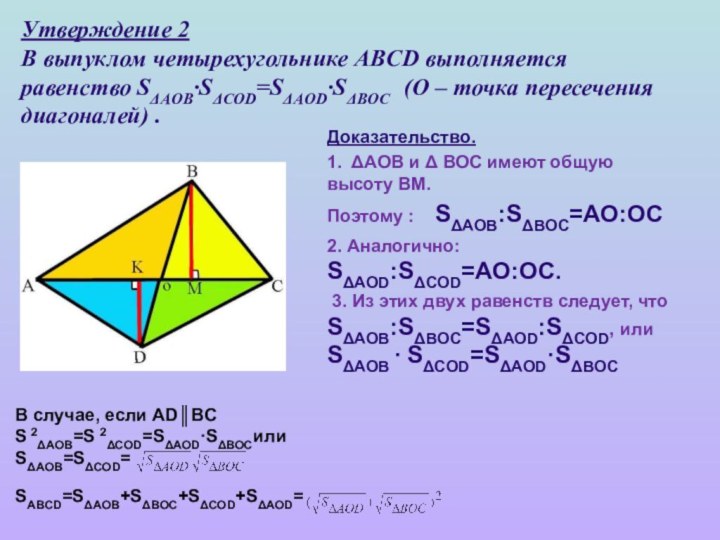
Слайд 18 Утверждение 2 В выпуклом четырехугольнике ABCD выполняется равенство SΔAOB·SΔCOD=SΔAOD·SΔBOC
(О – точка пересечения диагоналей) .
Доказательство.
1. ΔАОВ и
Δ ВОС имеют общую высоту ВМ.Поэтому : SΔAOB:SΔBOC=AO:OC
2. Аналогично: SΔAOD:SΔCOD=AO:OC.
3. Из этих двух равенств следует, что SΔAOB:SΔBOC=SΔAOD:SΔCOD, или SΔAOB · SΔCOD=SΔAOD·SΔBOC
В случае, если AD║BC
S 2ΔAOB=S 2ΔCOD=SΔAOD·SΔBOCили
SΔAOB=SΔCOD=
SABCD=SΔAOB+SΔBOC+SΔCOD+SΔAOD=
Слайд 19 Задача 5 В треугольнике АВС проведена медиана BD
, а через её середину и вершину А проведена
прямая AL. В результате такого построения треугольник АВС разбит на три треугольника и один четырехугольник. Найти площади этих фигур, если площадь АВС равна 60.Решение:
1. Так как BD – медиана, то SΔABD=SΔCBD=0,5SΔABC=30;
2. АО – медиана в треугольнике ABD, поэтому SΔAOB=SΔAOD=0,5SΔABD =15.
3. Продолжим медиану BD за точку D так, что DP=BD. Рассмотрим четырехугольник ABKP. По построению, BD=DP, тогда SΔABD=SΔADP=30.
4. Точка D стала точкой пересечения диагоналей четырехугольника ABCP, в которой они делятся пополам. Тогда ABCP – параллелограмм, т.е. AP║BK.
5. Значит, SΔPOK=SΔAOB=15.
6. В силу утверждения 2 можем заключить, что S 2ΔAOB =SΔAOP·SΔBOK.
Заметим, что SΔAOP=3SΔAOB=3·15=45, 225=45·SΔBOK, откуда SΔBOK=5.
Тогда SOKCD=60–30–5=25
Ответ: SΔAOB=SΔAOD =15; SΔBOK=5; SOKCD=25
Слайд 20 Задача 6 Диагонали выпуклого четырехугольника ABCD пересекаются в
точке Е, SABE=SCED. Площадь четырёхугольника ABCD больше площади треугольника
АВЕ не более чем в 4 раза. Найти CD, если АВ =Решение.
1. Так как SΔABE=SΔCED, тогда по утверждению 1 AD║BC.
2. Пусть SΔAED=S1, SΔBEC=S2.
Из утверждения 2 следует, что SΔABE=SΔCED= .
3. Так как
Значит,
4. Равенство имеет место только в том случае, когда
5.Значит, в силу утверждения1, заключаем, что AB║CD. Тогда ABCD – параллелограмм и CD=АВ=