- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятие о числе е, производная и первообразная показательной функции
Содержание
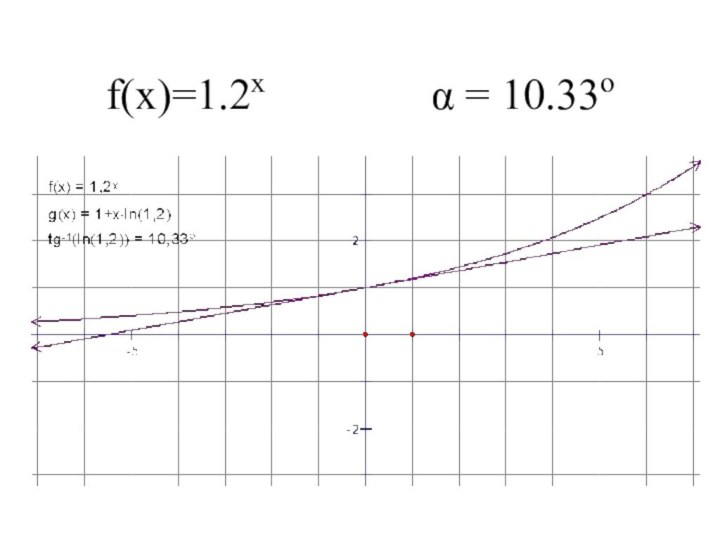
- 2. f(x)=1.2x α = 10.33o
- 3. f(x)= 1.5x α = 22.07o
- 4. f(x) = 2x α = 34.73o
- 5. f(x) = 2.2x α = 38.25o
- 6. f(x) = 2.5x α = 42.50o
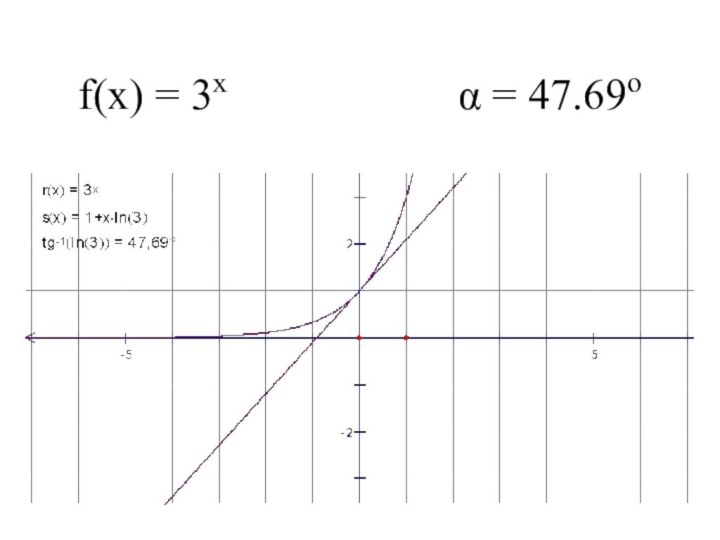
- 7. f(x) = 3x α = 47.69o
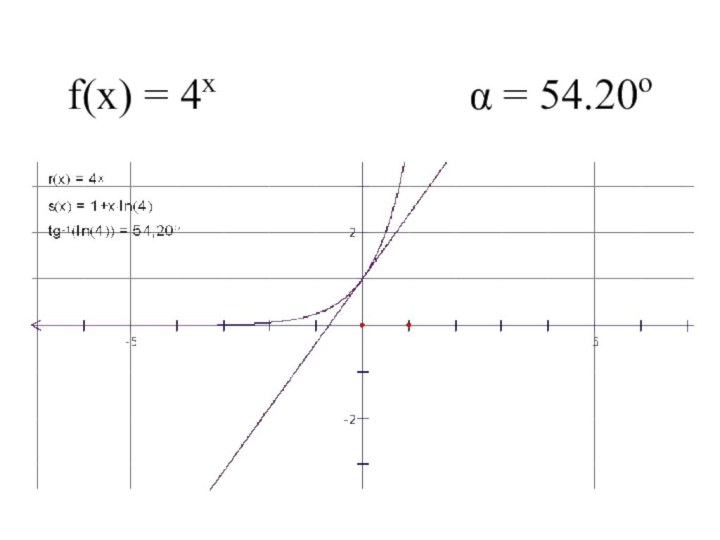
- 8. f(x) = 4x
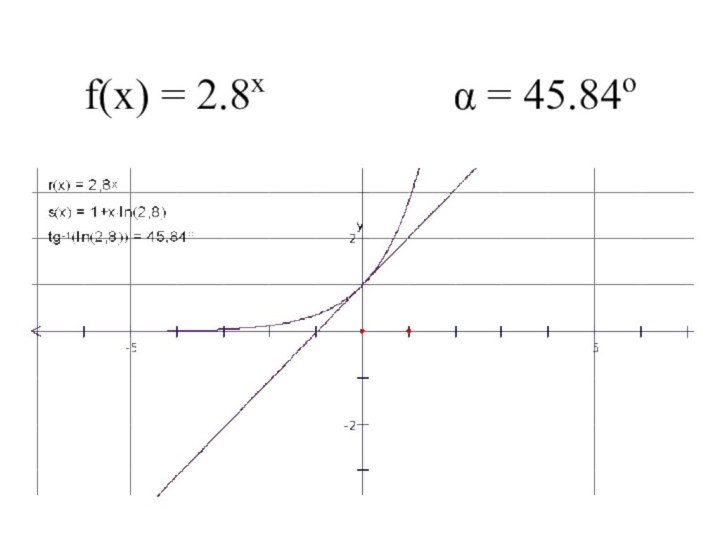
- 9. f(x) = 2.8x α = 45.84o
- 10. f(x) = 2.7x α = 44.81o
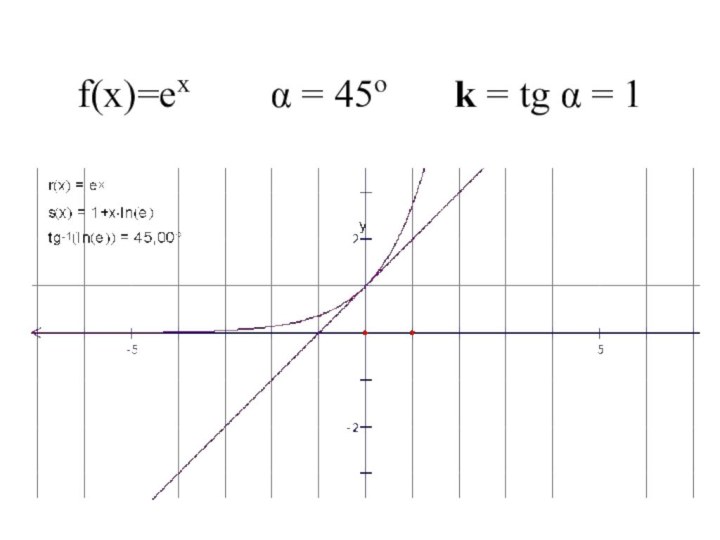
- 11. f(x)=ex α = 45o
- 12. Иррациональное число е.e = 2,7182818284590… бесконечная непериодическая десятичная дробьe ≈ 2,7
- 13. В пи – цифры не пересчитать,е –
- 14. Свойства функции у=еxD(y) = R;Функция общего
- 15. График касательной к графику функции у=еx в
- 16. Показательная функция у = ex в точке
- 17. Определение производной
- 18. Производная функции у=ех Нам задана функция
- 19. Любая первообразная для функции у(х) = ех
- 20. Натуральный логарифмНатуральным логарифмом называется логарифм по основанию е Обозначение: ln x = logex
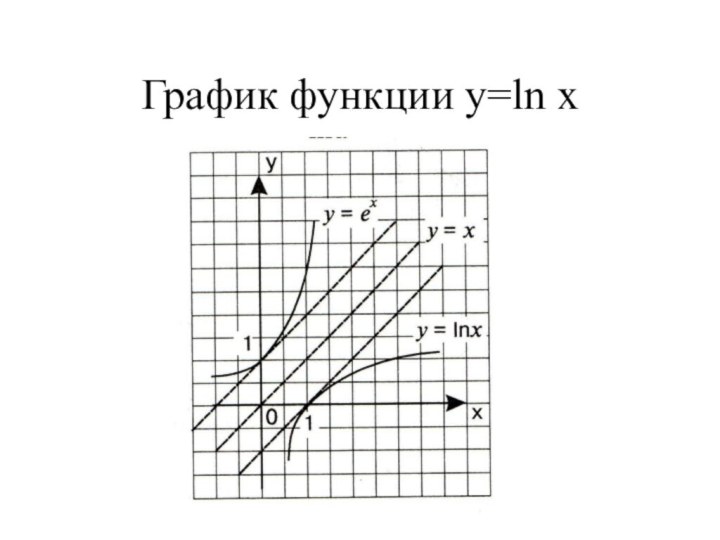
- 21. График функции y=ln x
- 22. Свойства функции у = ln xD(y) =
- 23. Производная показательной функции с произвольным основанием.a=elna ,
- 24. Скачать презентацию
- 25. Похожие презентации
f(x)=1.2x α = 10.33o

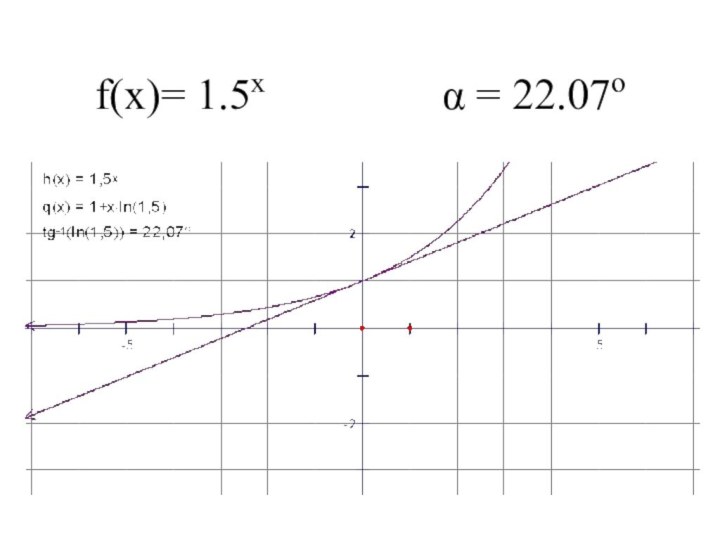
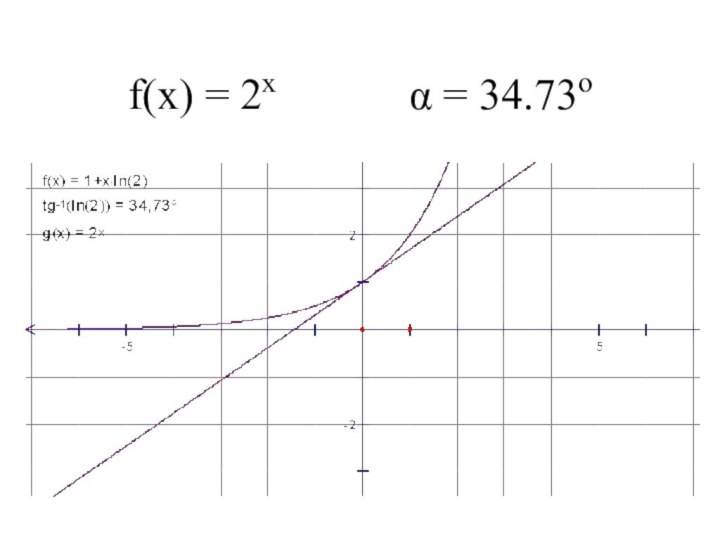
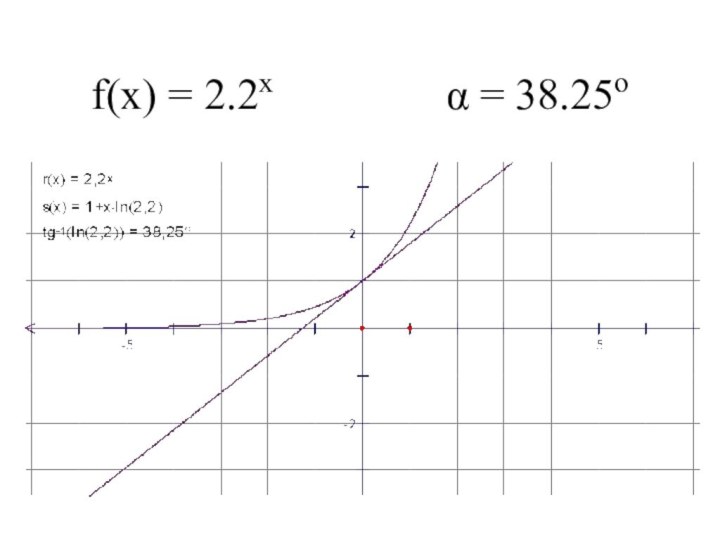
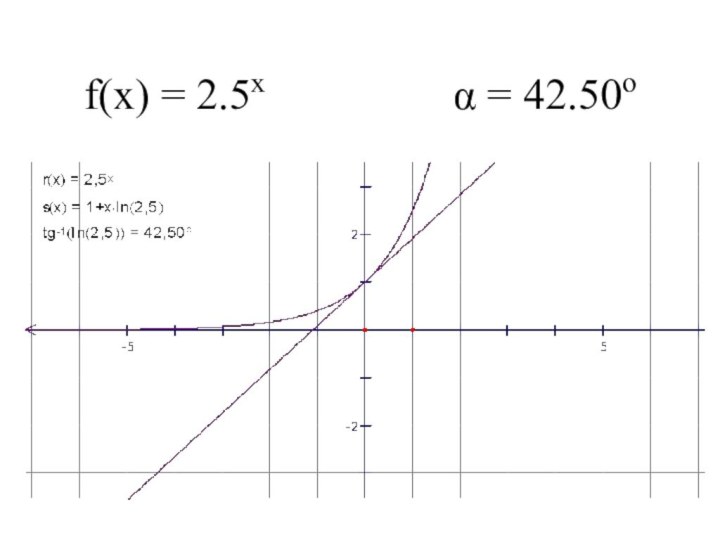






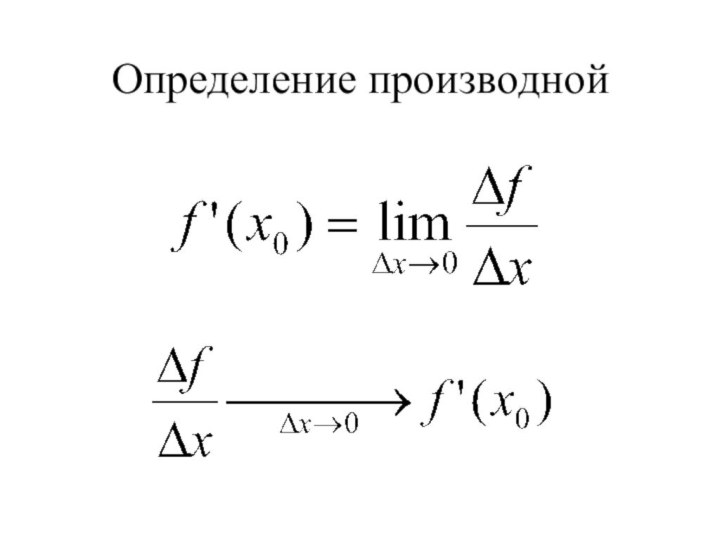






Слайд 12
Иррациональное число е.
e = 2,7182818284590…
бесконечная непериодическая десятичная дробь
e
≈ 2,7
Слайд 13
В пи – цифры не пересчитать,
е – бесконечно
столь же .
А если их с конца писать, какое
будет больше?
Слайд 14
Свойства функции у=еx
D(y) = R;
Функция общего вида;
Возрастает
на всей области определения;
Не имеет наибольшего и наименьшего значений;
Ограничена
снизу и неограничена сверху;Непрерывна;
Е(у) = (0 ;+ ∞);
Выпукла вниз;
Дифференцируема на всей области определения.
Слайд 15
График касательной к графику функции у=еx в точке
с абсциссой х=0, образует с положительным направлением оси абсцисс
угол в 45o.Угловой коэффициент касательной, проведенной к графику функции у=еx в точке с абсциссой х=0, равен 1
Слайд 18
Производная функции у=ех
Нам задана функция
у(x)=ех
у'(0) = 1, т.к. е0=1,
у(х) =ex
у(х+Δх) = ех+Δх,
Δу = у(х+Δх) - у(х) = ех+Δх - ех = ех (еΔх – 1),
пользуясь условием ( А) можем записать :
(ех)'= ех
Слайд 20
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию е
Обозначение: ln x = logex
Слайд 22
Свойства функции у = ln x
D(y) = (0
;+ ∞);
Функция общего вида;
Возрастает на всей области определения;
Не
имеет наибольшего и наименьшего значений;Неограничена снизу и сверху;
Непрерывна;
Е(у) = R;
Выпукла вверх;
Дифференцируема на всей области определения.