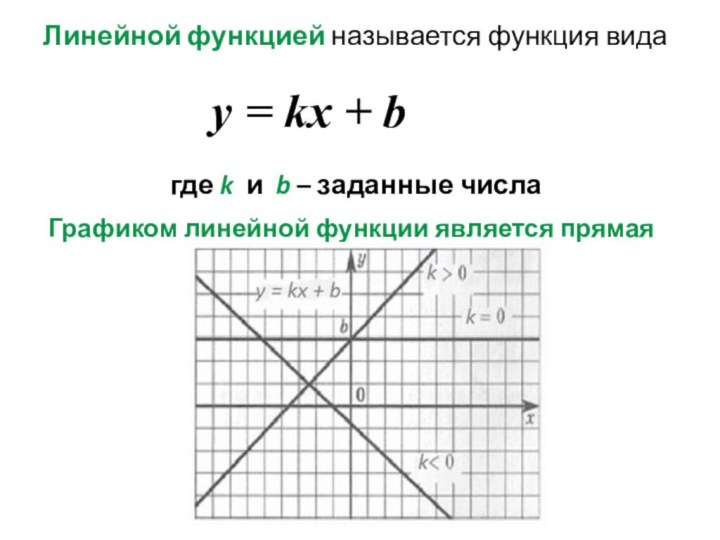
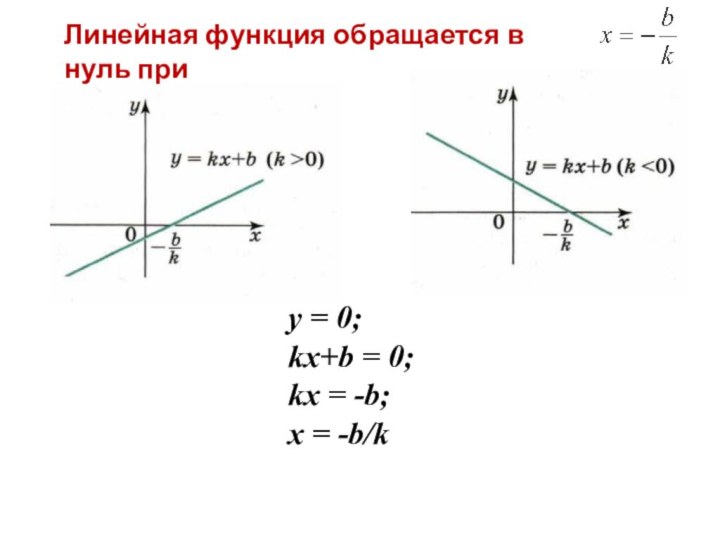
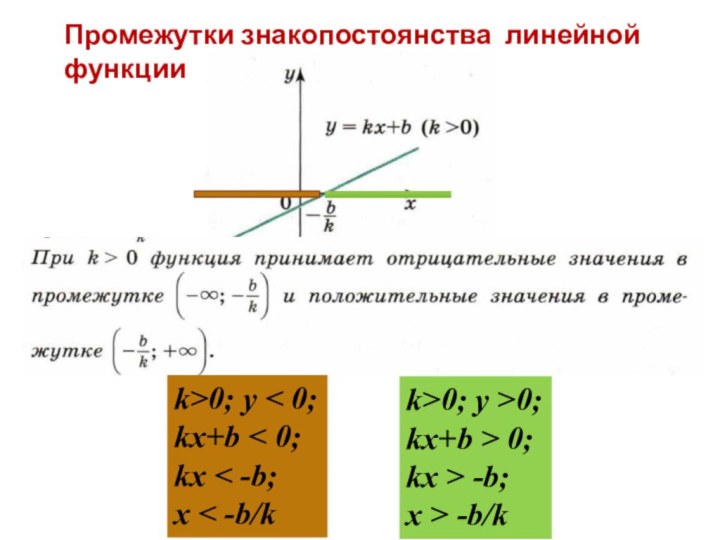
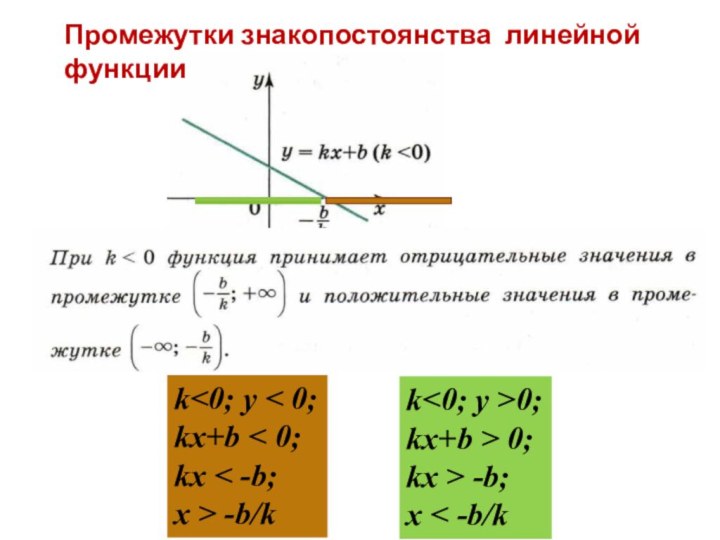
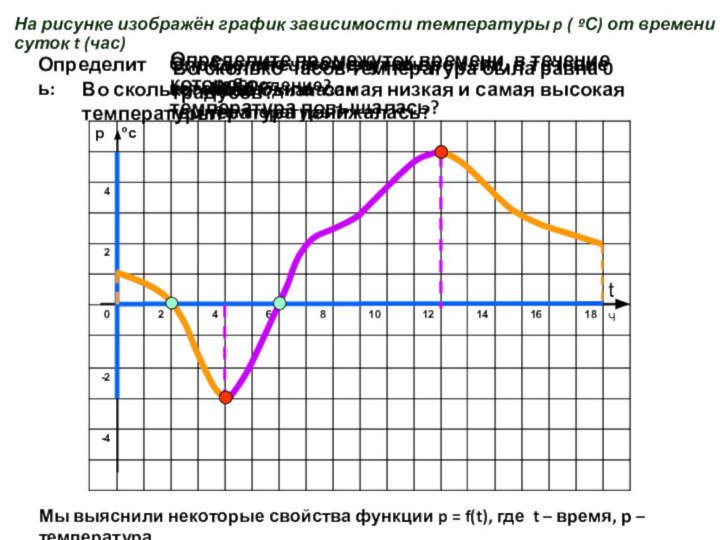
ºС) от времени суток t (час)
Определить:
Сколько часов длилось
наблюдение?Какой диапазон температуры?
Во сколько часов температура была равна 0 градусов?
Во сколько часов была самая низкая и самая высокая температуры?
Определите промежутки времени, в течение которых
температура понижалась?
Определите промежуток времени, в течение которого
температура повышалась?
Мы выяснили некоторые свойства функции p = f(t), где t – время, р – температура

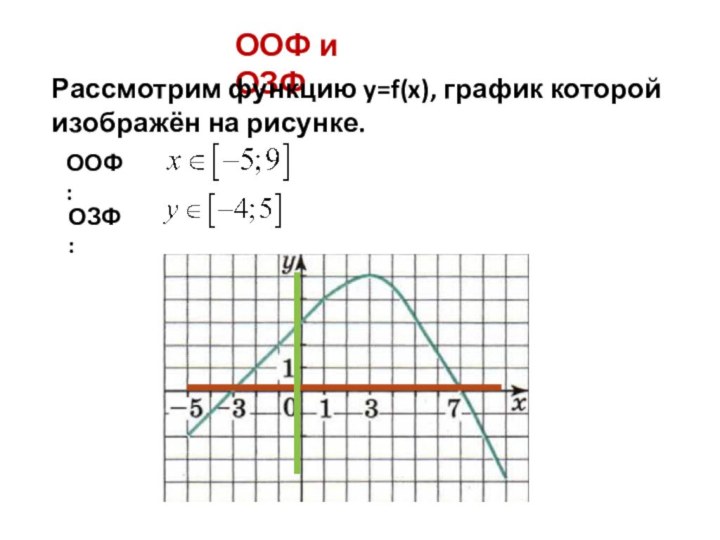
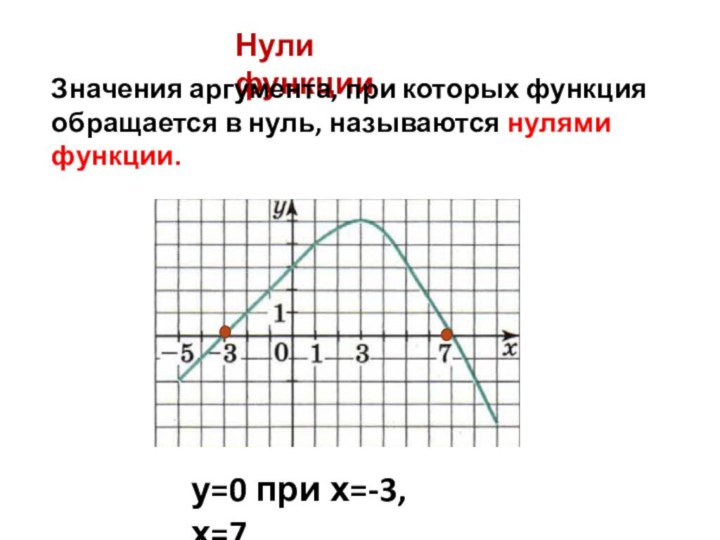
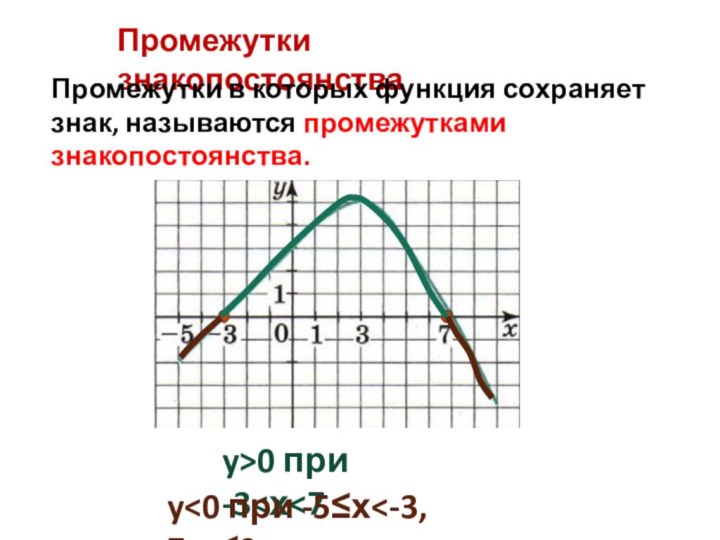

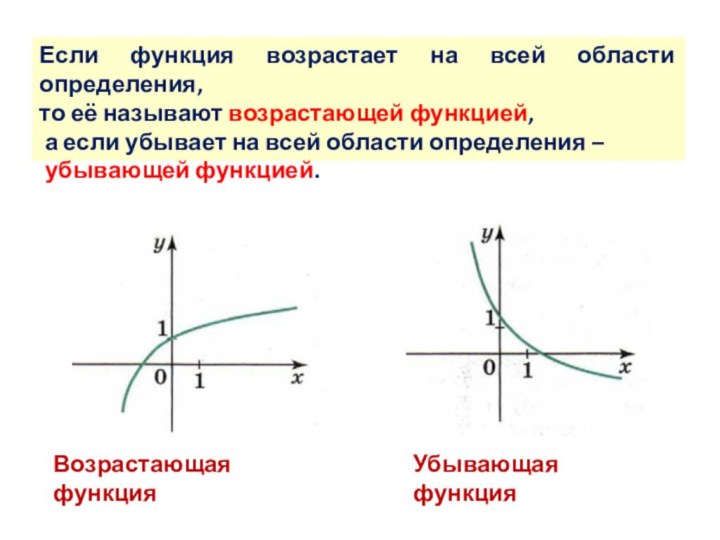
![Презентация по алгебре. Свойства функций Промежутки монотонностиФункция возрастает в промежуткеФункция убывает в промежутке[-5; 3].[3; 9].](/img/tmb/6/522361/3d6d26c712465d3ccf2e7de8fc9ed89f-720x.jpg)