- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Степенная функция
Содержание
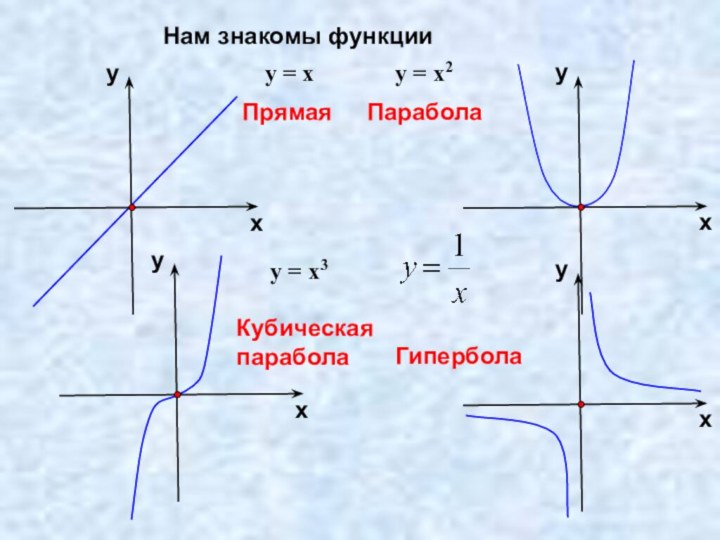
- 2. Нам знакомы функцииПрямаяПараболаКубическая параболаГиперболау = ху = х2у = х3
- 3. Все эти функции являются частными случаями степенной
- 4. Показатель – четное натуральное число (2n)10хуу =
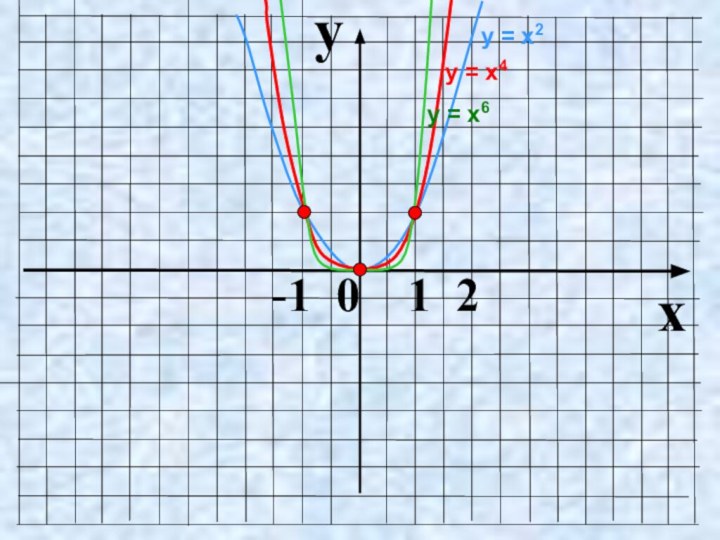
- 5. yx -1 0 1 2у = х2 у = х6у = х4
- 6. Показатель – нечетное натуральное число (2n-1)1хуу =
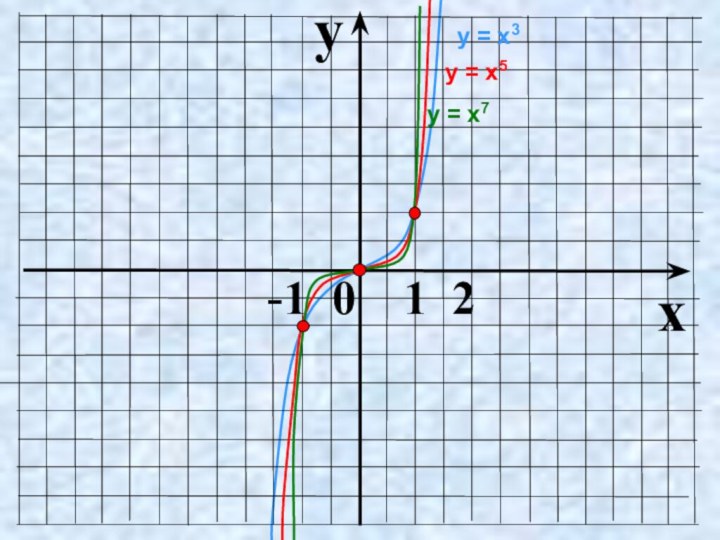
- 7. yx -1 0 1 2у = х3 у = х7у = х5
- 8. Показатель р = – (2n-1), где n
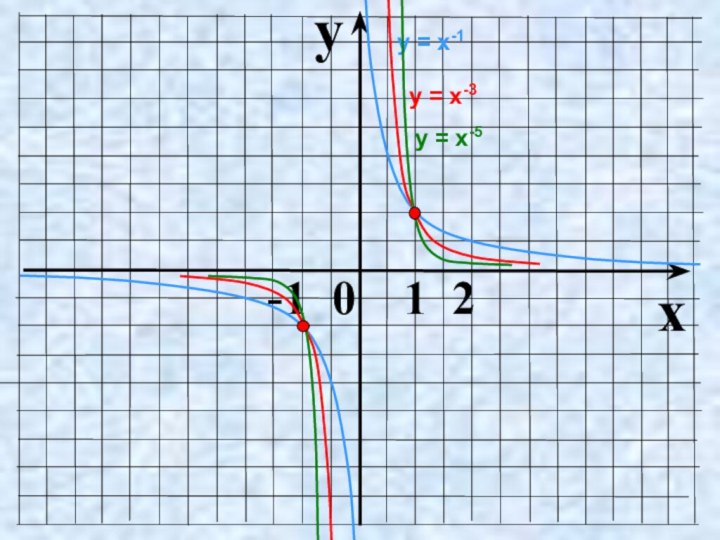
- 9. yx -1 0 1 2у = х-1у = х-3у = х-5
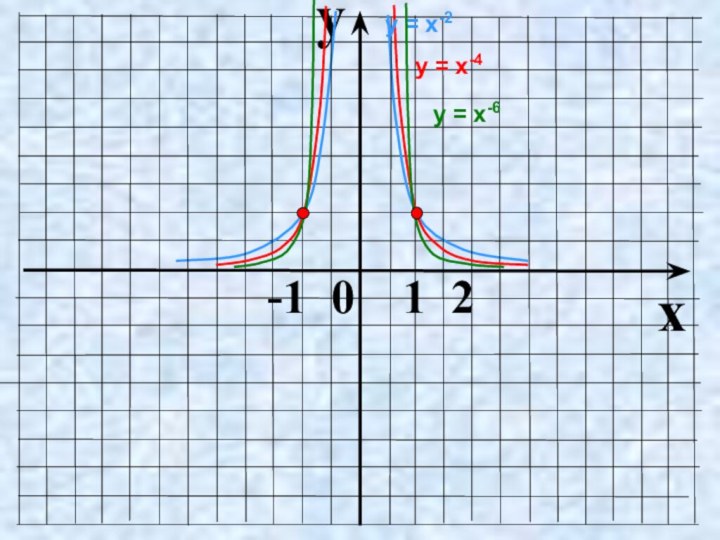
- 10. Показатель р = – 2n, где n
- 11. yx -1 0 1 2у = х-4у = х-2у = х-6
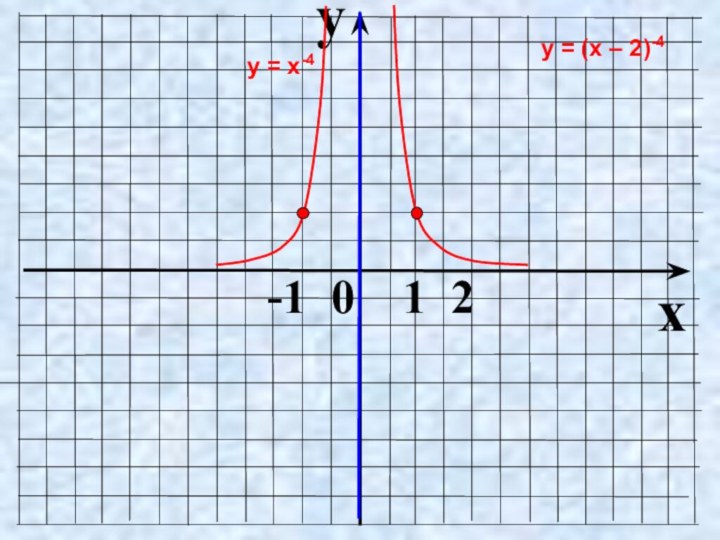
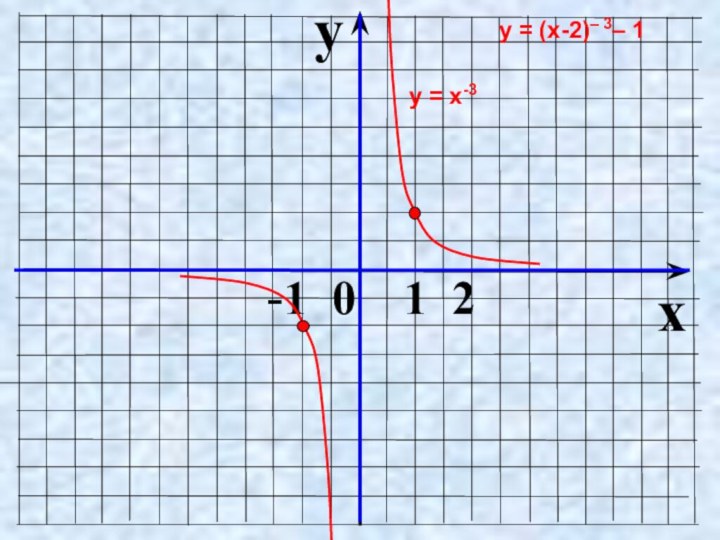
- 12. yx -1 0 1 2у = х-4у = (х – 2)-4
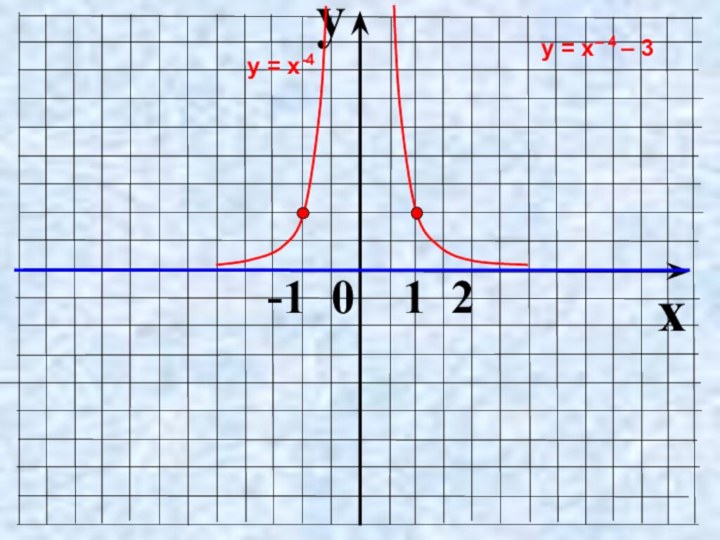
- 13. yx -1 0 1 2у = х-4у = х– 4 – 3
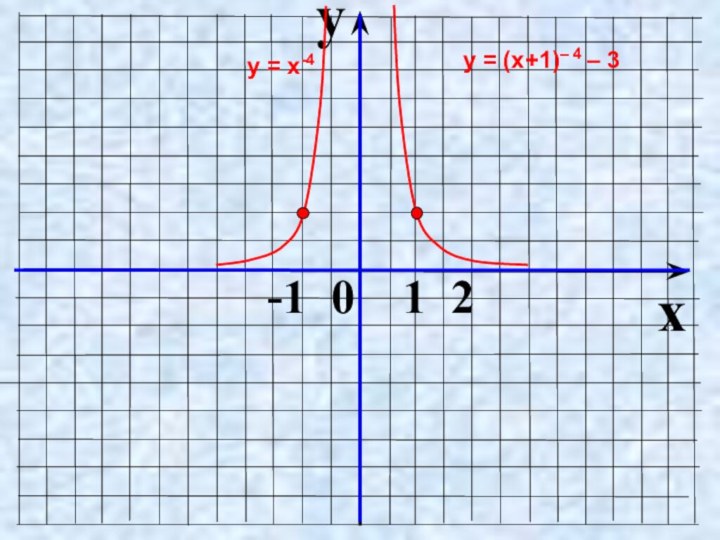
- 14. yx -1 0 1 2у = х-4у = (х+1)– 4 – 3
- 15. Скачать презентацию
- 16. Похожие презентации



Слайд 3
Все эти функции являются частными случаями степенной функции
у
= хn, у = х-n где n – заданное
натуральное числоСвойства и график степенной функции зависят от значения показателя n
Слайд 4
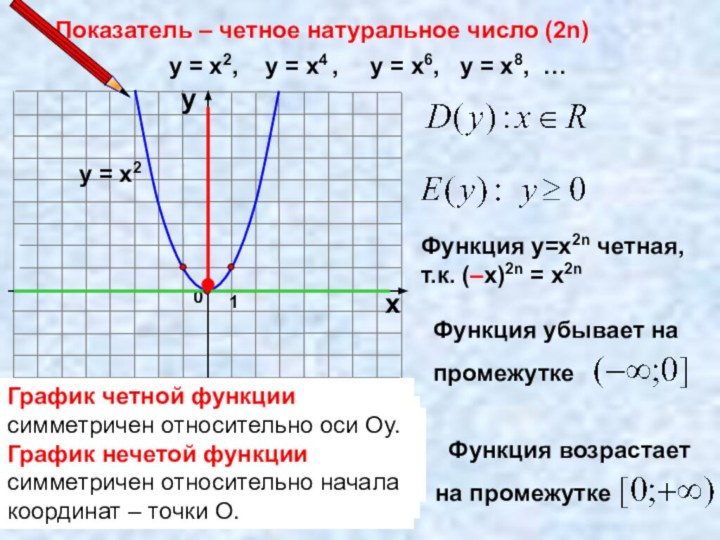
Показатель – четное натуральное число (2n)
1
0
х
у
у = х2,
у = х4 , у
= х6, у = х8, …у = х2
Функция у=х2n четная,
т.к. (–х)2n = х2n
Область определения функции –
значения, которые может принимать переменная х
Область значений функции –
множество значений,
которые может принимать
переменная у
График четной функции симметричен относительно оси Оу.
График нечетой функции симметричен относительно начала координат – точки О.
Слайд 6
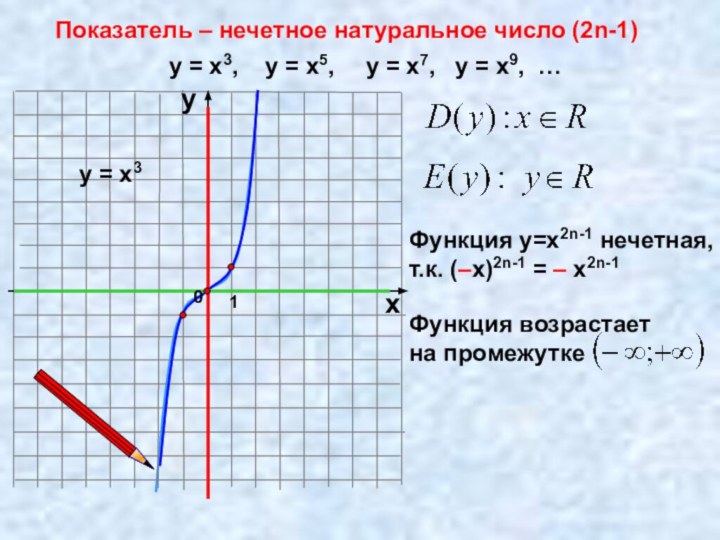
Показатель – нечетное натуральное число (2n-1)
1
х
у
у = х3,
у = х5, у =
х7, у = х9, …у = х3
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
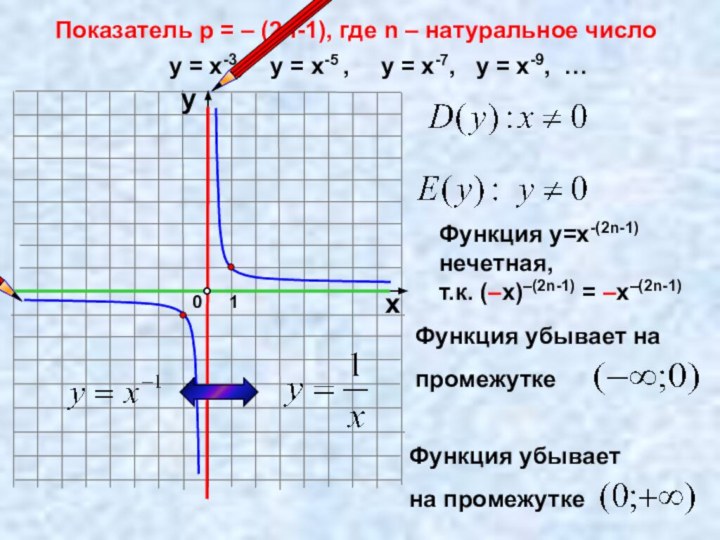
Слайд 8 Показатель р = – (2n-1), где n –
натуральное число
1
0
х
у
у = х-3, у = х-5 ,
у = х-7, у = х-9, … Функция у=х-(2n-1) нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Слайд 10 Показатель р = – 2n, где n –
натуральное число
1
0
х
у
у = х-2, у = х-4 ,
у = х-6, у = х-8, … Функция у=х2n четная,
т.к. (–х)-2n = х-2n