Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к уроку математики в 10 классе по теме Десятичные и натуральные логарифмы

Содержание

Цель урока:Формирование знаний по теме «Десятичные и натуральные логарифмы»
Десятичные и натуральные логарифмы Цель урока:Формирование знаний по теме «Десятичные и натуральные логарифмы» Задачи урока:Изучить понятие десятичного логарифма Изучить понятие натурального логарифмаРассмотреть свойства натурального логарифмаИзучить Заполните пропуски:Log? b + Logx ? = Log? (?a)Logx ? - Log? Десятичным логарифмом называется  логарифм по  основанию 10. 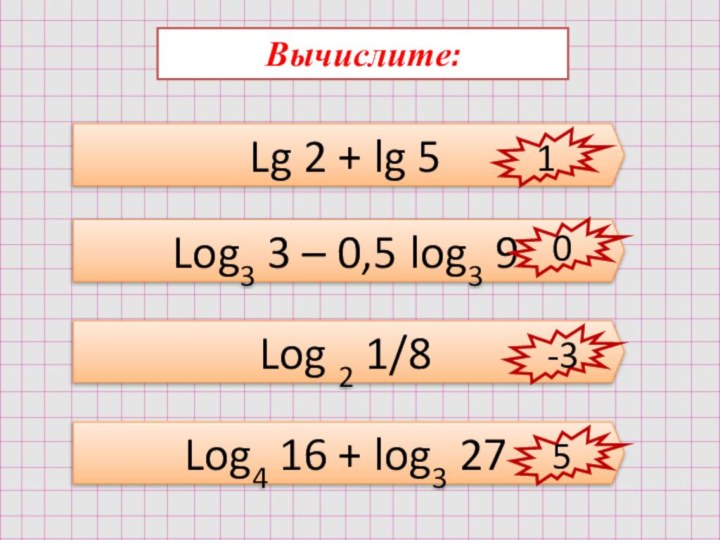Обозначается lg a Десятичный логарифм Десятичные логарифмыlog10 a=lg a Вычислите:Lg 2 + lg 5Log3 3 – 0,5 log3 9Log 2 1/8Log4 16 + log3 27 Натуральным логарифмом называется   логарифм по основанию  е Обозначается ln а Число е является иррациональным, его приближённое Формула перехода к новому основанию:   Перейти к основанию 2: Перейти к основанию 2: №305(1,2,3), №306(1) Итог урока: 1. Алимов Ш.А., Алгебра и начала математического анализа, Москва, Просвещение , 20172.https://nsportal.ru/shkola/algebra/library/2012/11/30/prezentatsiya-svoystva-logarifmov
Слайды презентации

Слайд 2 Цель урока:
Формирование знаний по теме «Десятичные и натуральные

Цель урока:Формирование знаний по теме «Десятичные и натуральные логарифмы»

логарифмы»

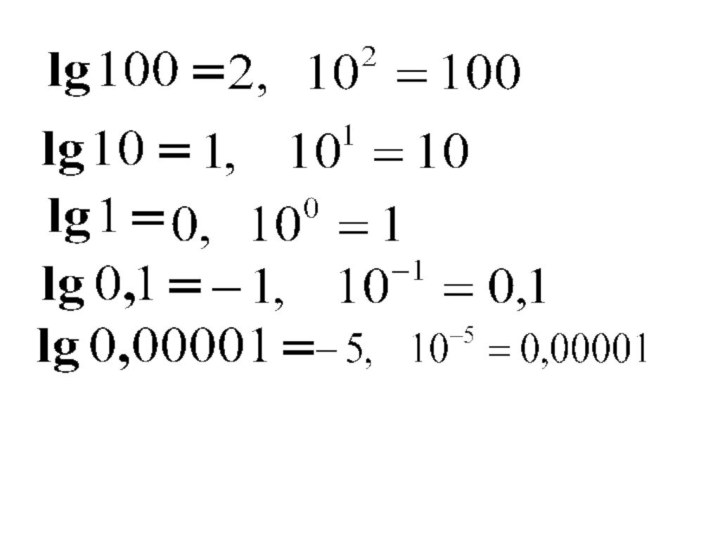
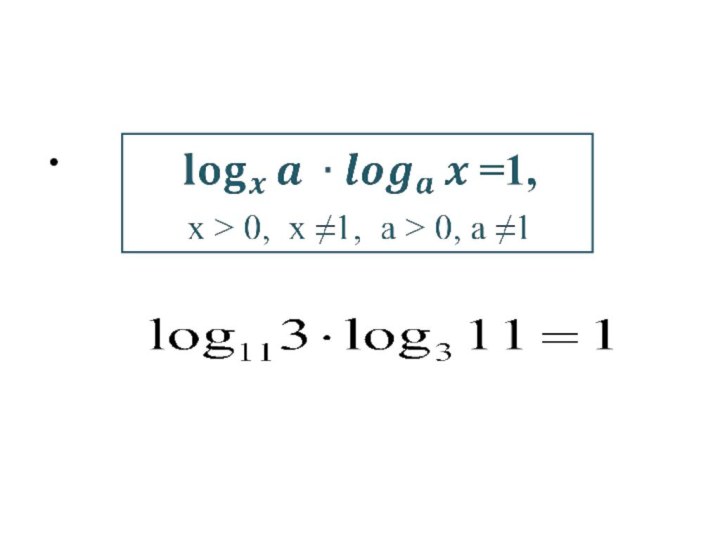
Слайд 3 Задачи урока:
Изучить понятие десятичного логарифма
Изучить понятие

Задачи урока:Изучить понятие десятичного логарифма Изучить понятие натурального логарифмаРассмотреть свойства натурального

натурального логарифма
Рассмотреть свойства натурального логарифма
Изучить формулу перехода к новому

основанию и закрепить ее

Слайд 4 Заполните пропуски:
Log? b + Logx ? = Log?

Заполните пропуски:Log? b + Logx ? = Log? (?a)Logx ? -

(?a)

Logx ? - Log? b = Log? (a/?)
Logx b?

= pLog? (?)

х

а

х

b

а

х

х

b

p

х

b

Слайд 5
Десятичным логарифмом называется  логарифм по  основанию 10.
Обозначается lg

Десятичным логарифмом называется  логарифм по  основанию 10. Обозначается lg a Десятичный логарифм

a
Десятичный логарифм чисел 0,1, 0,01, 0,001

равен соответственно -1, -2,-3,
т.е. имеют столько отрицательных  единиц сколько нулей стоит перед единицей, считая и ноль целых.

Слайд 6 Десятичные логарифмы
log10 a=lg a

Десятичные логарифмыlog10 a=lg a

Слайд 7

Слайд 8 Вычислите:
Lg 2 + lg 5
Log3 3 – 0,5

Вычислите:Lg 2 + lg 5Log3 3 – 0,5 log3 9Log 2 1/8Log4 16 + log3 27

log3 9
Log 2 1/8
Log4 16 + log3 27

Слайд 9
Натуральным логарифмом называется   логарифм по основанию  е
Обозначается ln а

Натуральным логарифмом называется   логарифм по основанию  е Обозначается ln а Число е является иррациональным, его




Число е является иррациональным, его приближённое значение 2.718281828. Значения

натуральных логарифмов можно вычислить только приближенно

Слайд 10

Слайд 11

Слайд 12 Формула перехода к новому основанию:

Формула перехода к новому основанию:

Слайд 13

Слайд 14
 


 

Слайд 15 Перейти к основанию 2:

Перейти к основанию 2:

Слайд 16 Перейти к основанию 2:

Перейти к основанию 2:

Слайд 17 №305(1,2,3), №306(1)

№305(1,2,3), №306(1)

Слайд 18 Итог урока:

Итог урока:
  • Имя файла: prezentatsiya-k-uroku-matematiki-v-10-klasse-po-teme-desyatichnye-i-naturalnye-logarifmy.pptx
  • Количество просмотров: 153
  • Количество скачиваний: 12
- Предыдущая Автоматизация звука [Ш].
Следующая -  Подвигу под Москвой - жить в веках!

Похожие презентации

Презентация по алгебре на темуПриведённое квадратное уравнение. Теорема Виета Презентация по алгебре на темуПриведённое квадратное уравнение. Теорема Виета 161
Презентация по математике на тему: Решение уравнения высших степеней (11 класс) Презентация по математике на тему: Решение уравнения высших степеней (11 класс) 61
Презентация к уроку по математике на тему Решение квадратных уравнений (9 класс) Презентация к уроку по математике на тему Решение квадратных уравнений (9 класс) 116
Презентация по алгебре на тему Решение задач на возрастание и убывание функции Презентация по алгебре на тему Решение задач на возрастание и убывание функции 149
Урок Уравнение касательной Урок Уравнение касательной 139
Преобразование выражений Преобразование выражений 183
КООРДИНАТНАЯ прямая КООРДИНАТНАЯ прямая 161
Координаты вектора 9 класс Координаты вектора 9 класс 181
Презентация: Прогрессии. Формулы, 9 класс Презентация: Прогрессии. Формулы, 9 класс 150
Презентация по математике на тему Тригонометрические уравнения. ОТбор корней в тринометрических уравнениях (11 класс) Презентация по математике на тему Тригонометрические уравнения. ОТбор корней в тринометрических уравнениях (11 класс) 69
Презентация по алгебре на тему Квадратичная функция. Презентация по алгебре на тему Квадратичная функция. 121
Исследование функции с помощью производной Исследование функции с помощью производной 129
Презентация по математике на тему Арифметический квадратный корень. Своя игра. 8 класс Презентация по математике на тему Арифметический квадратный корень. Своя игра. 8 класс 174
Техника дифференцирования. Производная сложной функции Техника дифференцирования. Производная сложной функции 108
Презентация: интеллектуальная игра по истории математики Пентагон Презентация: интеллектуальная игра по истории математики Пентагон 47
Презентация: Преобразование графиков функций (творческая проектная работа учащихся 10 класс) Презентация: Преобразование графиков функций (творческая проектная работа учащихся 10 класс) 56
Презентация по алгебре на тему Умножение дробей Презентация по алгебре на тему Умножение дробей 127
Понятие логического высказывания Понятие логического высказывания 119
Презентация к уроку математики в 7 классе Сравнение отрезков и углов Презентация к уроку математики в 7 классе Сравнение отрезков и углов 150
Упрощение выражений Упрощение выражений 182
Понятие вероятности. Практические задачи на вычисление вероятностей, (9 класс, ОГЭ) Понятие вероятности. Практические задачи на вычисление вероятностей, (9 класс, ОГЭ) 182
Золотое сечение. Золотое сечение. 135
Презентация к уроку алгебры по теме Формулы сокращенного умножения. Повторение. 7 класс. По учебнику С.М.Никольского Презентация к уроку алгебры по теме Формулы сокращенного умножения. Повторение. 7 класс. По учебнику С.М.Никольского 172
Ещё раз о квадратных уравнениях Ещё раз о квадратных уравнениях 157
Дробные рациональные уравнения Дробные рациональные уравнения 120
Шаблоны презентаций Математика - 7 Шаблоны презентаций Математика - 7 43
Наибольшее и наименьшее значения функции Наибольшее и наименьшее значения функции 121
Презентация К уроку математики в 11 классе. Подготовка к ЕГЭ. Решение текстовых задач. Презентация К уроку математики в 11 классе. Подготовка к ЕГЭ. Решение текстовых задач. 210
Производная степенной функции Производная степенной функции 121
Презентация Решение неравенств с помощью графика линейной функции Презентация Решение неравенств с помощью графика линейной функции 163