протяжении веков пытался постичь и создать порядок, красоту и
совершенство.”(Г. Вейль)
Г. Ессентуки Источник минеральной воды
Ватикан Площадь Святого Петра
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


















Г. Ессентуки Источник минеральной воды
Ватикан Площадь Святого Петра
Российский самолёт ТУ-154
Автомобиль
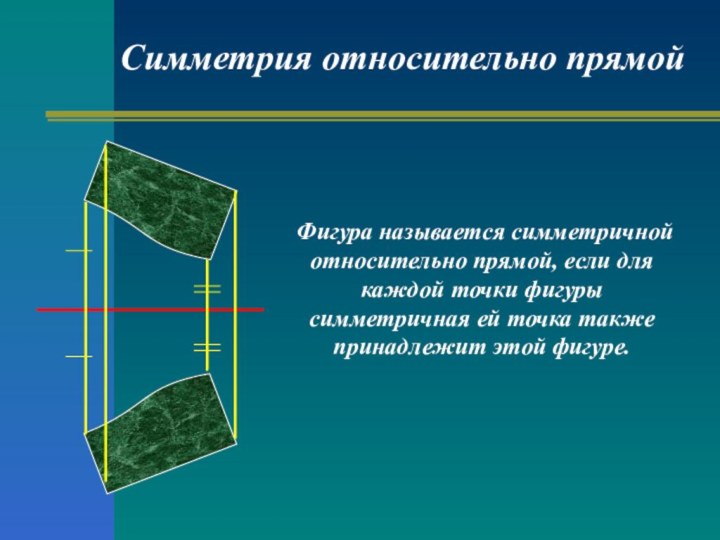
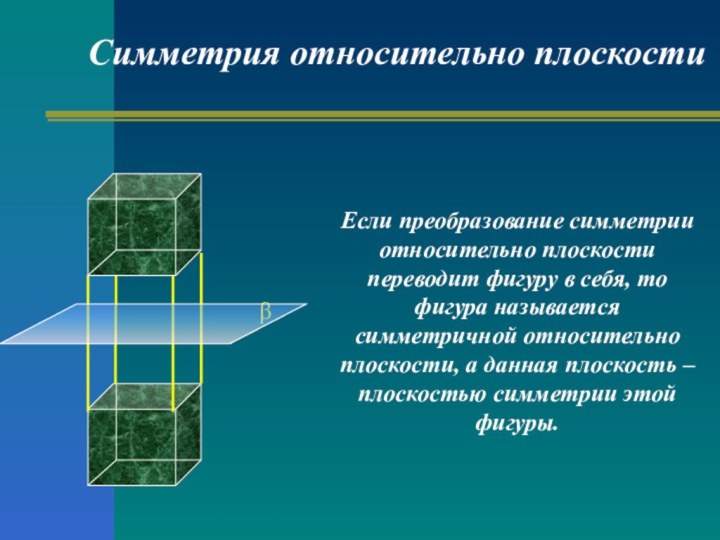
Симметрия относительно плоскости
β
Дубаи Башни Эмиратов
Соловецкий монастырь
Германия Гамбург
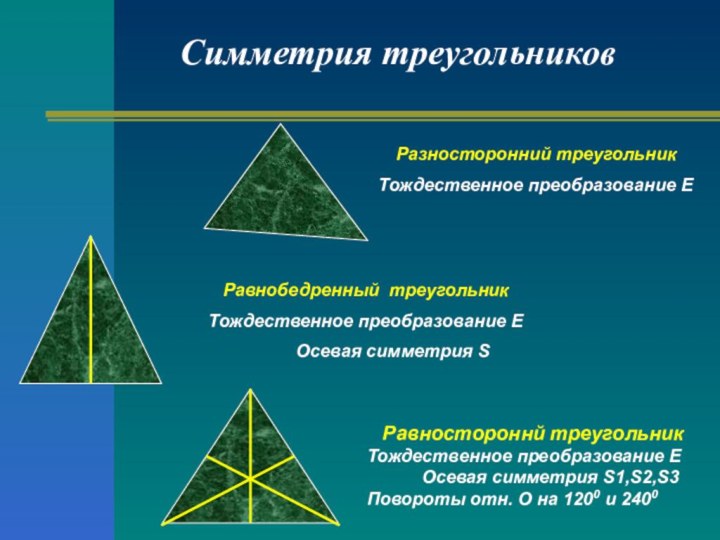
Разносторонний треугольник
Тождественное преобразование Е
Равнобедренный треугольник
Тождественное преобразование Е
Осевая симметрия S
1
2
3
Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.
Истинную красоту можно постичь только в единстве противоположностей
Москва Храм Христа Спасителя
Болгария София Александроневская лавра