Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему по алгебре на тему: Решение задач на сплавы (11 класс)

Содержание

2. Цели и задачи: личностные: формирование математической
3. Если вы хотите плавать, то смело входите
4. 1. Больному прописано лекарство, которое нужно пить
5. Налог на доходы составляет 13% от заработной
6. Ответ: 9 кг.х кг.(х+3) кг.(х+(х+3)) кг. Первый
7. Правило креста
8. Решение:10%40%30%20%10%х кгх+3 кгПервый сплав содержит 10% меди,
9. Имеется два сплава. Первый содержит 10% никеля,
10. Имеется два сплава. Первый содержит 10% никеля,
11. При смешивании 30 процентного раствора серной кислоты
12. Первый раствор содержит 40% кислоты, а второй
13. Первый сплав содержит 10% меди, второй –
14. Самостоятельная работа
15. Трехуровневое домашнее задание по карточкам (набор задач на смеси и сплавы)
16. Шел мудрец, а я навстречу ему три
17. 1. Кто во всем разобрался, смог решить
18. Спасибо за урок
19. Скачать презентацию
20. Похожие презентации

Цели и задачи: личностные: формирование математической грамотности учащихся; развитие навыков логического и творческого мышления предметные: повышение практической направленности предмета через решение практических задач; создание условий для систематизации, обобщения и углубления знаний учащихся

Главная
Алгебра
Презентация по алгебре на тему: Решение задач на сплавы (11 класс)

Урок математики в 11 классе Подготовка к ЕГЭ «Решение задач В11 на

Цели и задачи: личностные: формирование математической грамотности учащихся; развитие навыков

Если вы хотите плавать, то смело входите в воду, а если хотите

1. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза

Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича

Ответ: 9 кг.х кг.(х+3) кг.(х+(х+3)) кг. Первый сплав содержит 10% меди, второй

Решение:10%40%30%20%10%х кгх+3 кгПервый сплав содержит 10% меди, второй – 40% меди. Масса

Имеется два сплава. Первый содержит 10% никеля, второй- 30% никеля. Из этих

При смешивании 30 процентного раствора серной кислоты с10 процентным раствором серной кислоты

Первый раствор содержит 40% кислоты, а второй - 60% кислоты. Смешав эти

Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава

Трехуровневое домашнее задание по карточкам (набор задач на смеси и сплавы)

Шел мудрец, а я навстречу ему три человека, которые везли под горячим

1. Кто во всем разобрался, смог решить все предложенные задачи, и кто

Литература и интернет-ресурсыДенищева Л.О., Глазков Ю.А. и др. Единый Государственный экзамен

Слайды презентации

Слайд 2 Цели и задачи:
личностные: формирование математической грамотности учащихся;

Цели и задачи: личностные: формирование математической грамотности учащихся; развитие навыков логического

развитие навыков логического и творческого мышления предметные: повышение практической

направленности предмета через решение практических задач; создание условий для систематизации, обобщения и углубления знаний учащихся при решении текстовых задач.

Слайд 3 Если вы хотите плавать, то смело входите в

Если вы хотите плавать, то смело входите в воду, а если

воду, а если хотите научиться решать задачи, то решайте

их

Слайд 4 1. Больному прописано лекарство, которое нужно
пить по

1. Больному прописано лекарство, которое нужно пить по 0,5 г 3

0,5 г 3 раза в день в течение 21

дня.
В одной упаковке 10 таблеток лекарства по 0,5 г.
Какого наименьшего количества упаковок
хватит на весь курс лечения? ответ 7

1. Больному прописано лекарство, которое нужно
пить по 0,5 г 3 раза в день в течение 21 дня.
В одной упаковке 10 таблеток лекарства по 0,5 г.
Какого наименьшего количества упаковок
хватит на весь курс лечения?

2.На автозаправке клиент отдал кассиру 1000 рублей
и залил в бак 28 литров бензина по цене 28 руб. 50 коп.
за литр. Сколько рублей сдачи он должен
получить у кассира?

Слайд 5 Налог на доходы составляет 13% от заработной
платы.

Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана

Заработная плата Ивана Кузьмича равна
12500 рублей. Какую сумму он

получит после вычета
налога на доходы?
Ответ дайте в рублях.

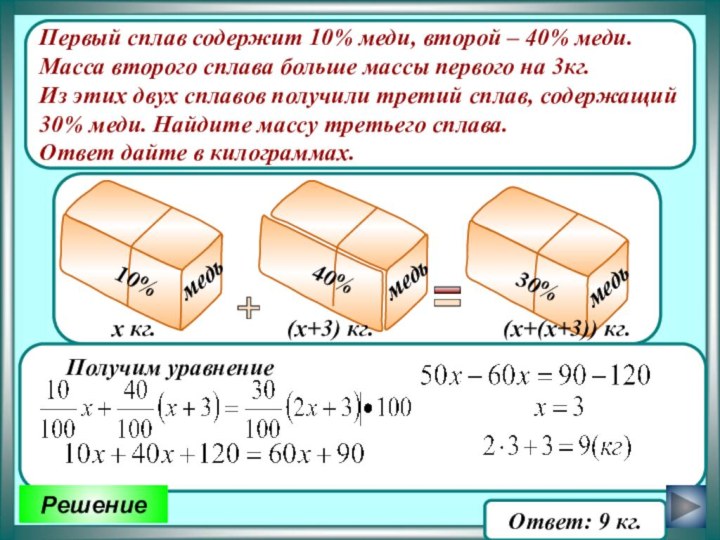
Слайд 6 Ответ: 9 кг.

х кг.
(х+3) кг.
(х+(х+3)) кг.

Первый сплав

Ответ: 9 кг.х кг.(х+3) кг.(х+(х+3)) кг. Первый сплав содержит 10% меди,

содержит 10% меди, второй – 40% меди.
Масса второго

сплава больше массы первого на 3кг.
Из этих двух сплавов получили третий сплав, содержащий
30% меди. Найдите массу третьего сплава.
Ответ дайте в килограммах.

Решение

Получим уравнение

Слайд 7 Правило креста

Слайд 8

Решение:

10%
40%
30%
20%
10%
х кг
х+3 кг

Первый сплав содержит 10% меди, второй

Решение:10%40%30%20%10%х кгх+3 кгПервый сплав содержит 10% меди, второй – 40% меди.

– 40% меди.
Масса второго сплава больше массы первого

на 3кг.
Из этих двух сплавов получили третий сплав, содержащий
30% меди. Найдите массу третьего сплава.
Ответ дайте в килограммах.

кг масса второго
сплава

кг масса третьего
сплава

кг масса первого

Первый сплав содержит 10% меди, второй – 40% меди.
Масса второго сплава больше массы первого на 3кг.
Из этих двух сплавов получили третий сплав, содержащий
30% меди. Найдите массу третьего сплава.
Ответ дайте в килограммах.

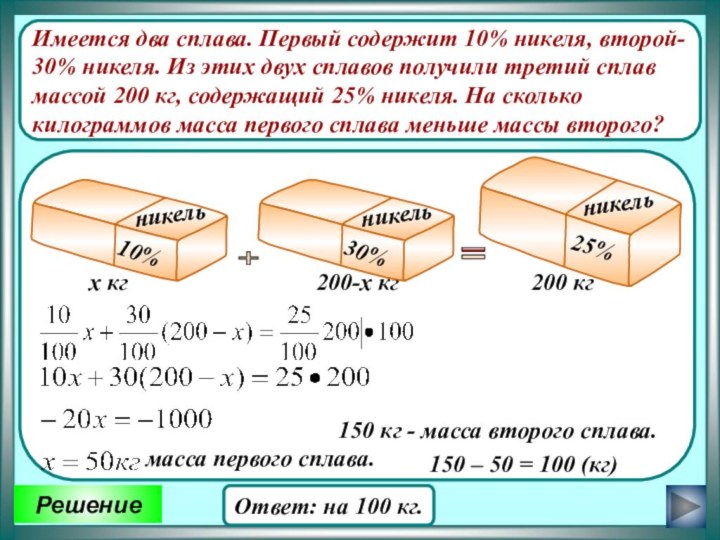
Слайд 9 Имеется два сплава. Первый содержит 10% никеля, второй-

Имеется два сплава. Первый содержит 10% никеля, второй- 30% никеля. Из

30% никеля. Из этих двух сплавов получили третий сплав

массой 200 кг, содержащий 25% никеля. На сколько
килограммов масса первого сплава меньше массы второго?

Решение

200 кг

х кг

Ответ: на 100 кг.

200-х кг

150 кг - масса второго сплава.

150 – 50 = 100 (кг)

масса первого сплава.

Слайд 10 Имеется два сплава. Первый содержит 10% никеля, второй-

30% никеля. Из этих двух сплавов получили третий сплав

массой 200 кг, содержащий 25% никеля. На сколько
килограммов масса первого сплава меньше массы второго?

кг масса 1 сплава

кг масса 2 сплава

Слайд 11 При смешивании 30 процентного раствора серной кислоты с
10

При смешивании 30 процентного раствора серной кислоты с10 процентным раствором серной

процентным раствором серной кислоты получилось 400 г
15 процентного раствора.

Сколько граммов 30 процентного
раствора было взято?

х г

Решение

400г.

(400-х)г

Ответ: 100 г.

Слайд 12 Первый раствор содержит 40% кислоты, а второй -

Первый раствор содержит 40% кислоты, а второй - 60% кислоты. Смешав

60% кислоты.
Смешав эти растворы и добавив 5 л

воды, получили 20 процентный
раствор. Если бы вместо воды добавили 5 л 80 процентного раствора,
то получился бы70 процентный раствор. Сколько литров 60 процентного
раствора кислоты было первоначально?

Решение

5 л

х л

у л

(х+у+5) л

0,40х (л) - кислоты в первом растворе

0,40х

0,60у (л) - кислоты во втором растворе

0,60у

0,20(х+у+5) л - кислоты в новом растворе

0,20(х+у+5)

0,80*5

0,70(х+у+5)

0,70(х+у+5) л - кислоты в новом растворе

Ответ: 2 л

Слайд 13 Первый сплав содержит 10% меди, второй – 40%

Первый сплав содержит 10% меди, второй – 40% меди. Масса второго

меди.
Масса второго сплава больше массы первого на 3кг.

Из этих двух сплавов получили третий сплав, содержащий
30% меди. Найдите массу третьего сплава.
Ответ дайте в килограммах.

Имеется два сплава. Первый содержит 10% никеля, второй-
30% никеля. Из этих двух сплавов получили третий сплав
массой 200 кг, содержащий 25% никеля. На сколько
килограммов масса первого сплава меньше массы второго?

При смешивании 30 процентного раствора серной кислоты с
10 процентным раствором серной кислоты получилось 400 г
15 процентного раствора. Сколько граммов 30 процентного
раствора было взято?

Слайд 14
Самостоятельная работа

Слайд 15
Трехуровневое домашнее задание по карточкам
(набор задач на

смеси и сплавы)

Слайд 16 Шел мудрец, а я навстречу ему три человека,

Шел мудрец, а я навстречу ему три человека, которые везли под

которые везли под горячим солнцем тележки с камнями для

строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил: «А что ты делал целый день?», тот ответил: «А я добросовестно выполнил свою работу.» А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»

Слайд 17 1. Кто во всем разобрался, смог решить все

1. Кто во всем разобрался, смог решить все предложенные задачи, и

предложенные задачи, и кто может помочь другим разобраться.

2.

Кто разобрался в задачах с одним условием, может составить уравнение и решить его.

3. Кто может составить только схему решения

(значит вы достигли цели, поставленной в
начале урока и можете поставить себе 5)

(вы что-то упустили, значит над поставленной целью надо еще поработать, но можете поставить себе 4)

(Вам нужно немного потрудиться и попробовать решить все задачи домашней работы. Вы также можете обратиться к тем ребятам, кто во все разобрался и получил 5.)