- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре Логарифмические уравнения
Содержание
- 2. Уравнения, в которых неизвестное находится под знаком логарифма, называются логарифмическими. Например: log2 x = 16
- 3. Методы решенияПо определению логарифма.Потенцирование.Введение новой переменной.Логарифмирование обеих частей уравнения.Приведение к одному основанию.Графически.
- 4. По определению логарифмаРешим уравнение : log2 x =
- 5. ПотенцированиеПотенцирование-это переход от уравнения вида logaf(x)=logag(x) к уравнению f(x)=g(x), где a>0 и а≠1,
- 6. Введение новой переменной.log52x+6log5x-7=0, где x >0Заменим log5x
- 7. Логарифмирование обеих частей уравнения.xlgx= 10000, ОДЗ: х>0Прологарифмируем
- 8. Приведение к одному основанию.log2x+log4x=0, приведем к одному основаниюlog2x+0,5log2x=01,5log2x=0x=1Ответ:1
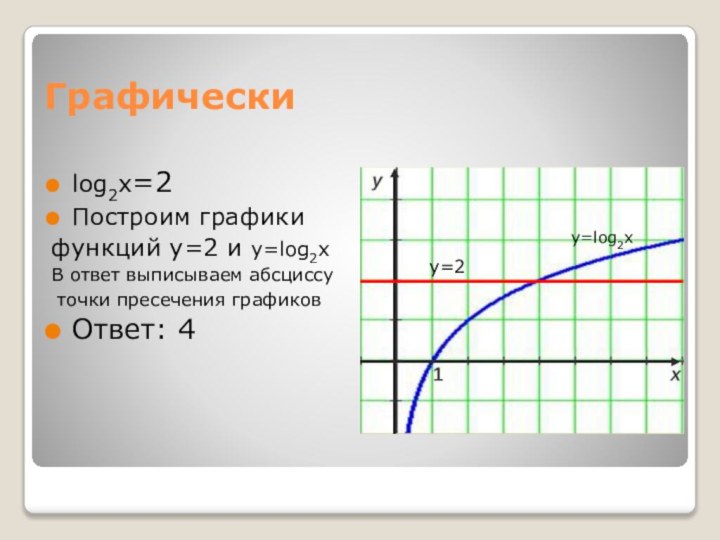
- 9. Графическиlog2x=2Построим графики функций y=2 и y=log2xВ ответ выписываем абсциссу точки пресечения графиковОтвет: 4y=2y=log2x
- 10. Скачать презентацию
- 11. Похожие презентации
Уравнения, в которых неизвестное находится под знаком логарифма, называются логарифмическими. Например: log2 x = 16









Слайд 2 Уравнения, в которых неизвестное находится под знаком логарифма,
называются логарифмическими.
Слайд 3
Методы решения
По определению логарифма.
Потенцирование.
Введение новой переменной.
Логарифмирование обеих частей
уравнения.
Приведение к одному основанию.
Графически.
Слайд 4
По определению логарифма
Решим уравнение : log2 x = 16
Вспомним
определение логарифма. Логарифмом положительного числа b по положительному и
отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b.То есть 2x=16
X = 4
Ответ : 4
Слайд 5
Потенцирование
Потенцирование-это переход от уравнения вида logaf(x)=logag(x) к уравнению f(x)=g(x), где a>0 и а≠1, а
f(x) и g(x) — элементарные алгебраические функции, f(x)>0,g(x)>0.
Например: log5(x+10)=log5(3x−6)
Уравнение имеет смысл при
(x+10) >0, т.е. x ∈ (-2, + ∞)
(3x−6) >0;
x+10=3x−6
2x=16
x=8
Ответ: 8
Слайд 6
Введение новой переменной.
log52x+6log5x-7=0, где x >0
Заменим log5x на
t, получаем t2-3t-4=0
по следствию из т.Виета получаем t1=-1,t2=4
Подставим:
log5x = -1 и log5x =4х=0,2 х= 625
Ответ: 0,2; 625
Слайд 7
Логарифмирование обеих частей уравнения.
xlgx= 10000, ОДЗ: х>0
Прологарифмируем обе
части уравнения по основанию 10:
lgxlgx =lg10000
lg2x=4
lgx=2 и
lgx=-2x=100 и x=0,01
Ответ: 0,01; 100.





























