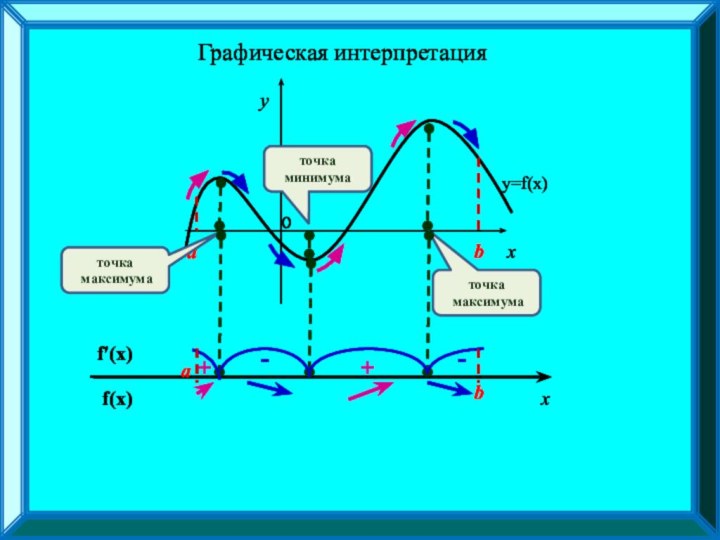
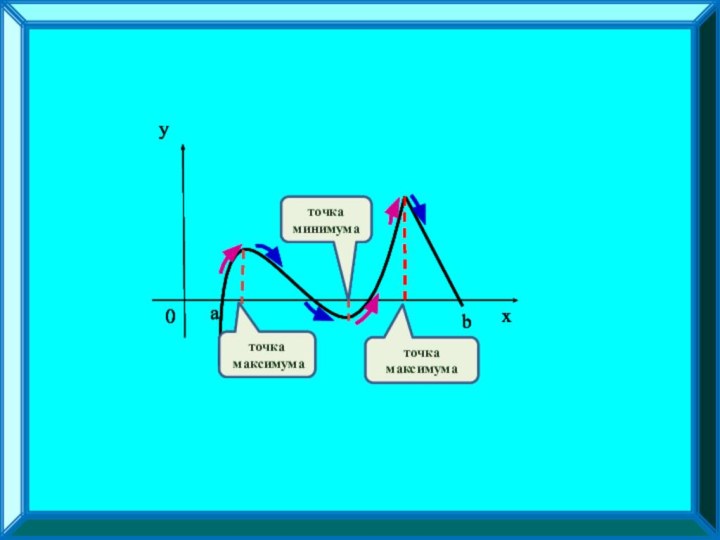
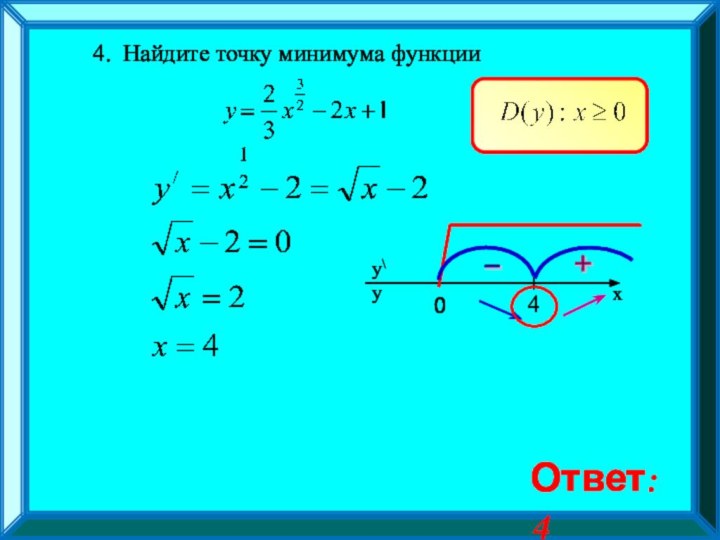
функции на возрастание/ убывание;
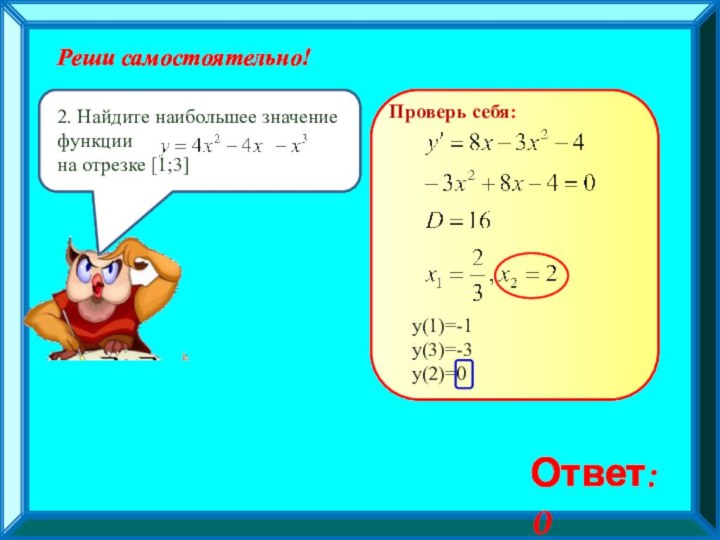
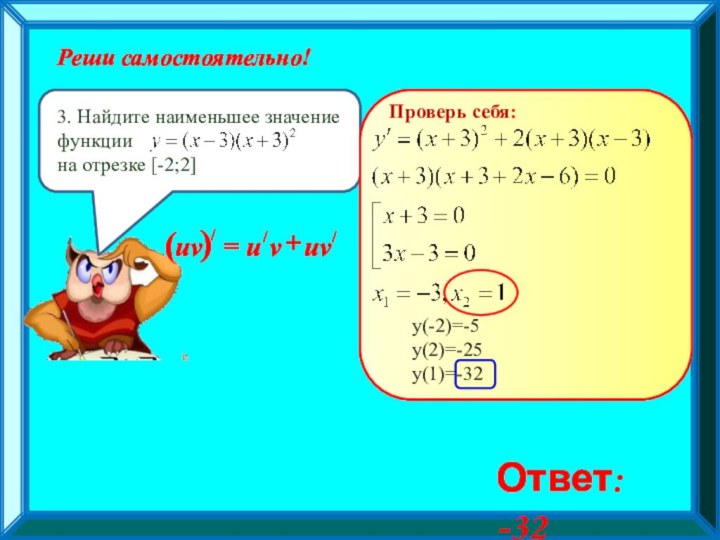
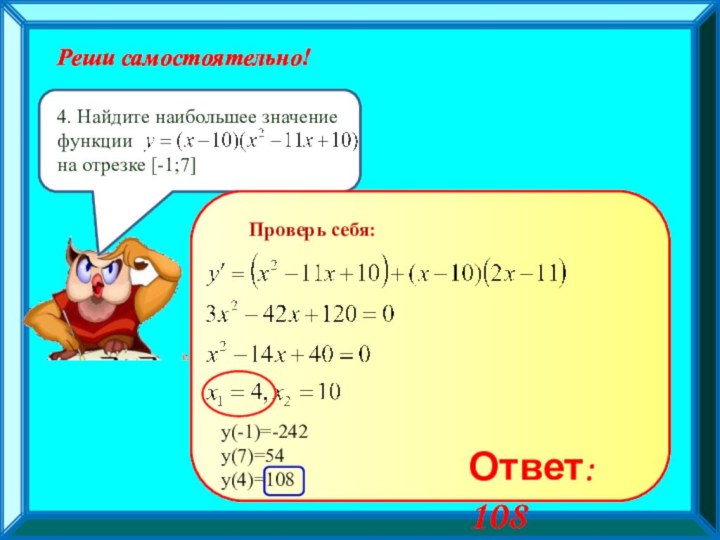
Исследование функции на наибольшие и наименьшие
значения на отрезке;Исследование функции с помощью графика ее производной (чтение графика производной)